
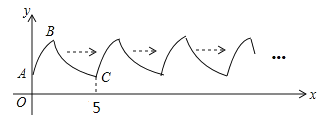
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
【答案】1 5
【解析】
由二次函数解析式可得点A坐标,由图象可知A、C之间的距离为5,即可判断点P与点A的纵坐标相同,由反比例函数图象可知在每个区间y随x的增大而减小,可得该“波浪线”上y的最大值为二次函数的最大值,把二次函数解析式配方成顶点式,可得函数最大值,即可得n的最大值.
∵抛物线解析式为![]() ,
,
∴x=0时,y=1,
∴点A坐标为(0,1)
由图象可知A、C之间的距离为5,
∴2020÷5=404,
∴点P与点A的纵坐标相同,
∴m=1,
由反比例函数图象可知,在每个区间y随x的增大而减小,
∴该“波浪线”上y的最大值为二次函数的最大值,
∵![]() =-4(x-1)2+5,
=-4(x-1)2+5,
∴该二次函数的最大值为5,
∴n的最大值为5.
故答案为:1,5


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
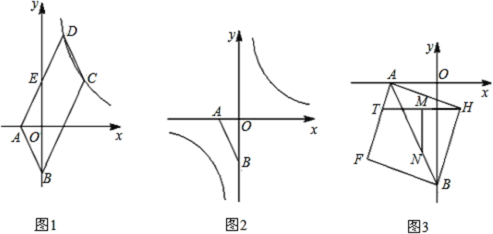
【题目】如图1,已知点![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 中点,双曲线
中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以点
轴上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,试求满足要求的所有点
为顶点的四边形是平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标;
的坐标;
(3)以线段![]() 为对角线作正方形
为对角线作正方形![]() (如图
(如图![]() ,点
,点![]() 是边
是边![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,
的中点,![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,
上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)求从中任意抽取1个球恰好是红球的概率;
(2)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙,你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
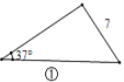

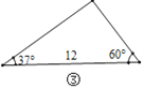
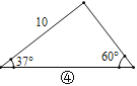
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____.
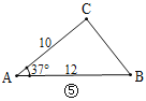
(2)如图⑤,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:
,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
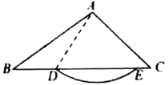
【题目】在![]() 中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称
中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称![]() 为
为![]() 的A-外截弧.例如,图中
的A-外截弧.例如,图中![]() 是
是![]() 的一条A-外截弧.在平面直角坐标系xOy中,已知
的一条A-外截弧.在平面直角坐标系xOy中,已知![]() 存在A-外截弧,其中点A的坐标为
存在A-外截弧,其中点A的坐标为![]() ,点B与坐标原点O重合.
,点B与坐标原点O重合.
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,满足条件的点C是_______.
中,满足条件的点C是_______.
(2)若点C在直线![]() 上.
上.
①求点C的纵坐标的取值范围.
②直接写出![]() 的A-外截弧所在圆的半径r的取值范围.
的A-外截弧所在圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
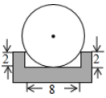
A.12 cmB.10 cmC.8 cmD.6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
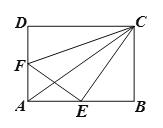
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)在(2)的条件下,求出![]() 的外接圆圆心与
的外接圆圆心与![]() 的外接圆圆心之间的距离?
的外接圆圆心之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
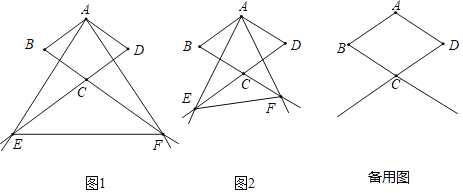
【题目】如图,菱形ABCD中,∠B=60°,AB=3cm,过点A作∠EAF=60°,分别交DC,BC的延长线于点E,F,连接EF.
(1)如图1,当CE=CF时,判断△AEF的形状,并说明理由;
(2)若△AEF是直角三角形,求CE,CF的长度;
(3)当CE,CF的长度发生变化时,△CEF的面积是否会发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com