
分析 (1)令y=0解方程即可求得A和B的横坐标,然后利用配方法即可求得对称轴和顶点坐标;
(2)首先求得D的坐标,然后利用面积公式即可求解.
解答 解:(1)令y=0,则-x2+2x+3=0,
解得:x1=-1,x2=3.
则A的坐标是(-1,0),B的坐标是(3,0).
y=-x2+2x+3=-(x-1)2+4,
则对称轴是x=1,顶点C的坐标是(1,4);
(2)D的坐标是(1,-4).
AB=3-(-1)=4,CD=4-(-4)=8,
则四边形ACBD的面积是:$\frac{1}{2}$AB•CD=$\frac{1}{2}$×4×8=16.
点评 本题考查了待定系数法求函数解析式以及配方法确定二次函数的对称轴和顶点坐标,正确求得A和B的坐标是关键.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{xy}{x^2}$ | B. | $\frac{2}{2x-2y}$ | C. | $\frac{x+y}{{{x^2}-{y^2}}}$ | D. | $\frac{2x}{x+2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
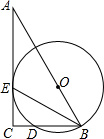 如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
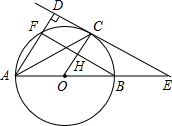 如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.
如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com