
【题目】如图,已知△ABC中,高为AD,角平分线为AE,若∠B=28°,∠ACD=52°,求∠EAD的度数. 
【答案】解:在△ABC中,∵∠ACD=∠B+∠BAC,
∴∠BAC=52°﹣28°=24°,
∵AE平分∠BAC,
∴∠BAE= ![]() ∠BAC=12°,
∠BAC=12°,
∴∠AED=∠B+∠BAE=28°+12°=40°,
∵AD为高,
∴∠ADE=90°,
∴∠EAD=90°﹣∠AED=90°﹣40°=50°
【解析】先根据三角形外角性质计算出∠BAC=24°,再根据角角平分线定义得到∠BAE= ![]() ∠BAC=12°,接着再利用三角形外角性质得到∠AED=∠B+∠BAE=40°,然后根据互余计算出∠EAD的度数.
∠BAC=12°,接着再利用三角形外角性质得到∠AED=∠B+∠BAE=40°,然后根据互余计算出∠EAD的度数.
【考点精析】根据题目的已知条件,利用三角形的内角和外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( ) 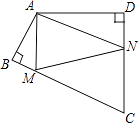
A.130°
B.120°
C.110°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
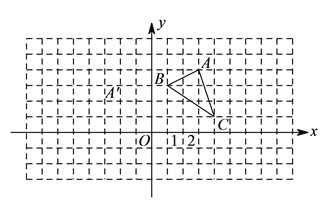
【题目】在平面直角坐标系中,![]() 的三个顶点位置如图所示,点
的三个顶点位置如图所示,点![]() 的坐标是
的坐标是![]() ,现将
,现将![]() 平移,使点
平移,使点![]() 移动到点
移动到点![]() ,且点
,且点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的对应点.
的对应点.
(![]() )请画出平移后的
)请画出平移后的![]() (不写画法).
(不写画法).
并直接写出点![]() ,
,![]() 的坐标:
的坐标:![]() ( ),
( ),![]() ( ).
( ).
(![]() )若三角形内部有一点
)若三角形内部有一点![]() ,则
,则![]() 的对应点
的对应点![]() 的坐标是
的坐标是![]() ( ).
( ).
(![]() )如果坐标平面内有一点
)如果坐标平面内有一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形,请直接写出点
为顶点的四边形为平行四边形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850

对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)求m,n的值;
(2)补全频数分布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组?
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP⊥AD于P点. 
求证:
(1)△BAE≌△ACD;
(2)∠BQP=60°;
(3)BQ=2PQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com