
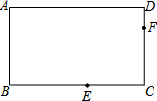 在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F.若AD=$\sqrt{3}$AB=$\sqrt{3}$,则AF2=( )
在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F.若AD=$\sqrt{3}$AB=$\sqrt{3}$,则AF2=( )| A. | 8-4$\sqrt{3}$ | B. | 10-4$\sqrt{3}$ | C. | 8+4$\sqrt{3}$ | D. | 10+4$\sqrt{3}$ |
分析 由AD=$\sqrt{3}$AB=$\sqrt{3}$,可求得AB=1,AD=$\sqrt{3}$,又由在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,根据轴对称的性质,可求得BE,CF的长,继而求得DF的长,然后由勾股定理求得答案.
解答 解:∵AD=$\sqrt{3}$AB=$\sqrt{3}$,
∴AB=1,AD=$\sqrt{3}$,
∵四边形ABCD是矩形,
∴BC=AD=$\sqrt{3}$,CD=AB=1,
∵在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,
∴BE=AB=1,
∴CF=CE=BC-BE=$\sqrt{3}$-1,
∴DF=CD-CF=2-$\sqrt{3}$,
∴AF2=AD2+DF2=($\sqrt{3}$)2+(2-$\sqrt{3}$)2=10-4$\sqrt{3}$.
故选B.
点评 此题考查了矩形的性质、轴对称的性质以及勾股定理.注意掌握轴对称图形的对应关系.


科目:初中数学 来源: 题型:选择题
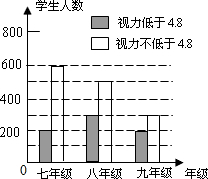 某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )| A. | 本次抽查活动共抽查了2100名学生 | |
| B. | 本次抽查活动中视力不低于4.8的学生人数占总人数的66.7% | |
| C. | 本次抽查活动中视力不低于4.8学生人数中的极差为300人 | |
| D. | 由活动结果可以知道随着年级的增长,视力低于4.8的人数越来越多,呈上升趋势,那么同年级中抽到视力不低于4.8的学生的概率将越来越小 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
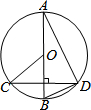 如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )| A. | 25° | B. | 20° | C. | 65° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com