Question

【题目】如图1，在等边△ABC中，点D是边AC的中点，点P是线段DC上的动点（点P与点C不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，连接AA1 ， 射线AA1分别交射线PB、射线B1B于点E、F．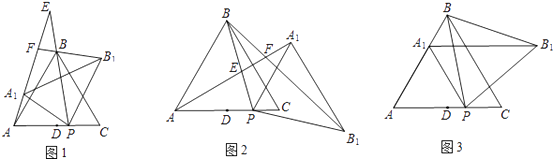
（1）如图1，当0°＜α＜60°时，在α角变化过程中，△BEF与△AEP始终存在关系（填“相似”或“全等”），并说明理由；
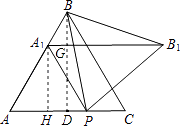
（2）如图2，设∠ABP=β．当60°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；
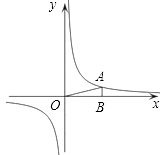
（3）如图3，当α=60°时，点E、F与点B重合．已知AB=4，设DP=x，△A1BB1的面积为S，求S关于x的函数关系式．

Answer 1

【答案】
（1）相似
（2）解：存在，理由如下：

∵∠PAE=∠EBF，∠AEP=∠BEF，

∴△BEF∽△AEP，

若要使得△BEF≌△AEP，只需要满足BE=AE即可，

∴∠BAE=∠ABE，

∵∠BAC=60°，

∴∠BAE= ，

∵∠ABE=β，∠BAE=∠ABE，

∴ ，

即α=2β+60°

（3）解：连接BD，交A1B1于点G，

过点A1作A1H⊥AC于点H．

∵∠B1A1P=∠A1PA=60°，

∴A1B1∥AC，

由题意得：AP=A1P=2+x，∠A=60°，

∴△PAA1是等边三角形，

∴A1H=sin60°A1P= ，

在Rt△ABD中，BD= ，

∴BG= ，

∴ （0≤x＜2）．

【解析】解：（1）相似 由题意得：∠APA1=∠BPB1=α，AP=A1P，BP=B1P，
则∠PAA1=∠PBB1= ，
∵∠PBB1=∠EBF，
∴∠PAE=∠EBF，
又∵∠BEF=∠AEP，∠EBF=∠EAP，
∴△BEF∽△AEP；
【考点精析】关于本题考查的相似三角形的判定与性质和旋转的性质，需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了才能得出正确答案．