Question

17．阅读下面的材料：在平面几何中，我们学过两条直线互相垂直的定义，下面就两个一次函数的图象所确定的两条直线，给出它们相互垂直的定义：设一次函数y=k₁x+b₁（k₁≠0）的直线为l₁，一次函数y=k₂x+b₂（k₂≠0）的图象为直线l₂．若k₁•k₂=-1，我们就称直线l₁与直线l₂相互垂直，现请解答下面的问题：已知直线l与直线y=-$\frac{1}{2}$x-1互相垂直，且直线l的图象过点P（-1，4），且直线l分别与y轴、x轴交于A、B两点．
（1）求直线l的函数表达式；
（2）若点C是线段AB上一动点，求线段OC长度的最小值；
（3）若点Q是AO上的一动点，求△BPQ周长的最小值，并求出此时点Q的坐标；
（4）在（3）的条件下，若点P关于BQ的对称点为P′，请求出四边形ABOP′的面积．

Answer 1

分析 （1）设直线l的解析式为y=kx+b，由垂直的定义可求得直线l中的k，再把P点坐标代入可求得b，可求得直线l的解析式；
（2）过O作OC⊥AB，此时OC最小，可先求得BC长，再利用面积相等可求得OC的长；
（3）可求得点P关于y轴的对称点P″，连接BP″交y轴于点Q，则Q点即为所求，可求得直线BP″解析式，则可求得Q点坐标；
（4）由对称可求得P′点的坐标，可分别求得△AOB和△AOP′的面积，可求得四边形ABOP′的面积．

解答 解：
（1）设直线l的解析式为y=kx+b，
∵直线l与直线y=-$\frac{1}{2}$x-1互相垂直，
∴-$\frac{1}{2}$k=-1，解得k=2，
∵直线l的图象过点P（-1，4），
∴-k+b=4，即-2+b=4，解得b=6，
∴直线l的解析式为y=2x+6；
（2）如图1，过O作OC⊥AB于点C，
此时线段OC的长度最小，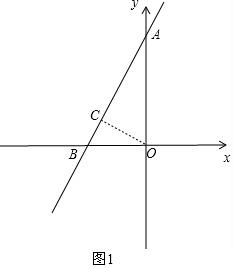

在y=2x+6中，令x=0可得y=6，令y=0可求得x=-3，
∴A（0，6），B（-3，0），
∴OA=6，OB=3
∴AB=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$，
∵$\frac{1}{2}$AB•OC=$\frac{1}{2}$OA•OB，
∴3$\sqrt{5}$OC=3×6，
∴OC=$\frac{6\sqrt{5}}{5}$，
即线段OC长度的最小值为$\frac{6\sqrt{5}}{5}$；
（3）如图2，作点P关于y轴的对称点P″，连接BP″交y轴于点Q，过P″作P″G⊥x轴于点G，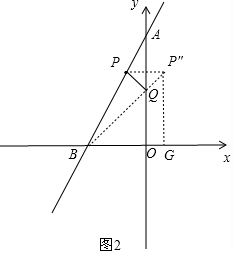

则PQ=P″Q，
∴PQ+BQ=BQ+QP″，
∵点B、Q、P″三点在一条线上，
∴BQ+PQ最小，
∵P（-1，4），
∴P″（1，4），
∴P″G=4，OG=1，
∴BG=BO+OG=4=P″G，
∴∠OBQ=45°，BP″=4$\sqrt{2}$，
∴OQ=BO=3，
∴Q点坐标为（0，3），
又BP=$\sqrt{（3-1）^{2}+{4}^{2}}$=2$\sqrt{5}$，
此时△BPQ的周长=BP+BP″=4$\sqrt{2}$+2$\sqrt{5}$；
（4）由（3）可知∠OBQ=∠OQB=45°，
∴∠PQA=∠P″QA=45°，
∴PQ⊥BQ，
如图3，延长PQ到点P′，使PQ=P′Q，则P′即为点P关于BQ的对称点，过P′作P′H⊥y轴于点H，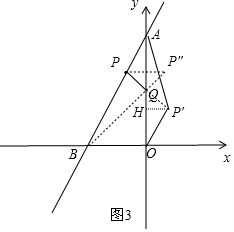

由（3）可知PQ=QP′=$\sqrt{2}$，
∴QH=HP′=1，
∴OH=OQ-QH=3-1=2，
∴S_{四边形ABOP′}=S_△AOB+S_△AOP′=$\frac{1}{2}$×6×3+$\frac{1}{2}$×6×1=12，
即四边形ABOP′的面积为12．

点评 本题为一次函数综合应用，涉及待定系数法、勾股定理、轴对称、等腰直角三角形及三角形的面积等知识点．在（1）中利用好题目中所给的定义是解题的关键，在（2）中利用垂线段最短确定出点C的位置是解题的关键，在（3）中利用对称确定出Q点的位置是解题的关键，在（4）中求得P′的坐标是解题的关键．本题考查知识点较多，综合性较强，难度适中．