
 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.分析 (1)先证明△ADE∽△ABC,然后利用相似比可求出$\frac{AE}{AC}$的值;
(2)先证明△ADE∽△ABC,然后利用相似比可求出BC的长.
解答 解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{4}{4+8}$=$\frac{1}{3}$;
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$,即$\frac{3}{BC}$=$\frac{1}{3}$,
∴BC=9.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.在运用相似三角形的性质时主要利用相似比计算线段的长.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )| A. | ∠AED=∠B | B. | ∠ADE=∠C | C. | $\frac{AD}{DE}=\frac{AC}{BC}$ | D. | $\frac{AD}{AC}=\frac{AE}{AB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
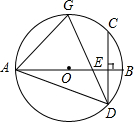 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AB}$的中点,连结AD,AG,CD,则下列结论不一定成立的是( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AB}$的中点,连结AD,AG,CD,则下列结论不一定成立的是( )| A. | CE=DE | B. | ∠ADG=∠GAB | C. | ∠AGD=∠ADC | D. | ∠GDC=∠BAD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | (-$\frac{1}{2}$,-1) | D. | (2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下面的材料:在平面几何中,我们学过两条直线互相垂直的定义,下面就两个一次函数的图象所确定的两条直线,给出它们相互垂直的定义:设一次函数y=k1x+b1(k1≠0)的直线为l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2.若k1•k2=-1,我们就称直线l1与直线l2相互垂直,现请解答下面的问题:已知直线l与直线y=-$\frac{1}{2}$x-1互相垂直,且直线l的图象过点P(-1,4),且直线l分别与y轴、x轴交于A、B两点.
阅读下面的材料:在平面几何中,我们学过两条直线互相垂直的定义,下面就两个一次函数的图象所确定的两条直线,给出它们相互垂直的定义:设一次函数y=k1x+b1(k1≠0)的直线为l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2.若k1•k2=-1,我们就称直线l1与直线l2相互垂直,现请解答下面的问题:已知直线l与直线y=-$\frac{1}{2}$x-1互相垂直,且直线l的图象过点P(-1,4),且直线l分别与y轴、x轴交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com