
【题目】如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OA和OC是方程x![]() (3+
(3+![]() )x+3
)x+3![]() =0的两根(OA>OC),∠CAO=30°,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
=0的两根(OA>OC),∠CAO=30°,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
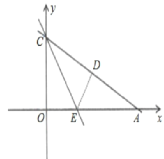
(1)求点D的坐标;
(2)设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、D. C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
【答案】(1)D(![]() ,
,![]() );(2)M(
);(2)M(![]() ,
,![]() );
);
【解析】
(1)由折纸可以知道CD=OC,从而求出AD,作DF⊥OA于F解直角三角形可以求出D点的坐标.
(2)存在满足条件的M点,利用三角形全等和平行线等分线段定理可以求出M点对应的坐标.
(1) 解方程x![]() (3+
(3+![]() )x+3
)x+3![]() =0得:
=0得:
x![]() =
=![]() ,x
,x![]() =3
=3
∵OA>OC
∴OA=3,OC=![]() ;
;
在Rt△AOC中,由勾股定理得:
AC=![]() =2
=2![]() ,
,
由轴对称得:CO=CD=![]() ,作DF⊥OA于F,
,作DF⊥OA于F,
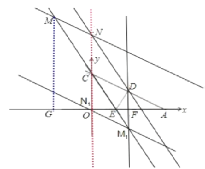
∴AD=![]() ,作DF⊥OA,且∠CAO=30°,
,作DF⊥OA,且∠CAO=30°,
∴DF=![]() ,由勾股定理得:
,由勾股定理得:
AF=![]() ,
,
∴OF=![]() ,∴OF=AF
,∴OF=AF
∴D(![]() ,
,![]() );
);
(2)∵M![]() N
N![]()
∠N![]() M
M![]() F=∠ADF,∠FN
F=∠ADF,∠FN![]() M
M![]() =∠FAD
=∠FAD
∵OF=AF
∴△ADF≌△N![]() M
M![]() F(AAS),
F(AAS),
∴M![]() F=DF=
F=DF=![]() ,N
,N![]() F=AF=
F=AF=![]() ,
,
∴M![]() (
(![]() ,
, ![]() ),作MG⊥OA,
),作MG⊥OA,
∵四边形MCDN和四边形CN![]() M
M![]() D是平行四边形
D是平行四边形
∴MC=ND,ND=CM![]() ∴MC=CM
∴MC=CM![]()
∴GO=OF=![]() ,OE=1
,OE=1
∴GE=![]() ,
,
∴EOC△∽△EGM
∴![]()
∴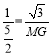 解得:
解得:
MG=![]() ,
,
∴M(![]() ,
,![]() )
)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )

A. 13B. 16C. 8D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
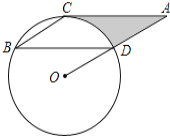
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=4![]() .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x![]() 2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
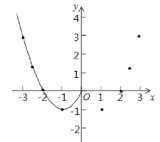
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
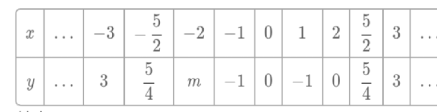
其中,m=___.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有___个交点,所以对应的方程x![]() 2|x|=0有___个实数根;
2|x|=0有___个实数根;
②方程x![]() 2|x|=
2|x|=![]() 有___个实数根;
有___个实数根;
③关于x的方程x![]() 2|x|=a有4个实数根时,a的取值范围是___.
2|x|=a有4个实数根时,a的取值范围是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三江夜游项目是宁波市月光经济和“三江六岸”景观提升的重要工程,一艘游轮从周宿夜江游船码头到宁波大剧院游船码头顺流而行用40分钟,从宁波大剧院游船码头沿原线返回周宿夜江游船码头用了1小时,已知游轮在静水中的平均速度为8千米/小时,求水流的速度.设水流的速度为x千米/小时,则可列方程为( )
A.40(8-x)=1×(8+x) B.![]() (8+x)=8 C.
(8+x)=8 C.![]() (8+x)=8-x D.
(8+x)=8-x D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
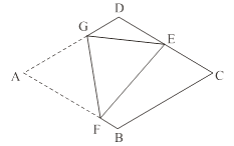
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
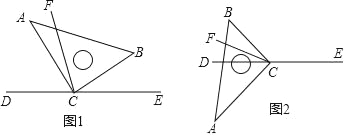
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
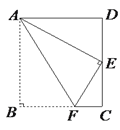
【题目】如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处, 折痕为AF,若CD=6,则AF等于__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com