
����Ŀ���ڡ�ABC�У���ACB=30�㣬����ABC�Ƶ�B����ʱ�뷽����ת���õ���A1BC1 �� 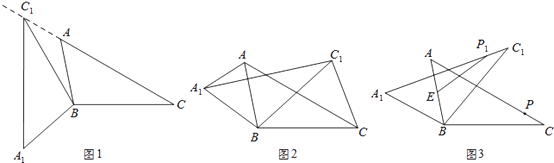
��1����ͼ1������C1���߶�CA���ӳ���ʱ�����CC1A1�Ķ�����
��2����֪AB=6��BC=8��
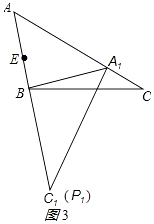
����ͼ2������AA1 �� CC1 �� ����CBC1�����Ϊ16�����ABA1�������
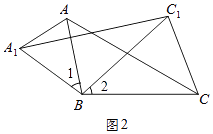
����ͼ3����EΪ�߶�AB�е㣬��P���߶�AC�ϵĶ��㣬�ڡ�ABC�Ƶ�B����ʱ�뷽����ת�Ĺ����У���P�Ķ�Ӧ�ǵ�P1 �� ֱ��д���߶�EP1���ȵ����ֵ��
��3���߶�EP1���ȵ����ֵΪ11���������£�
���𰸡�
��1��
�⣺������ã���A1C1B�ա�ACB��
��BC1=BC����A1C1B=��C=30�㣬
���BC1C=��C=30�㣬
���CC1A1=60��
��2��
�⣺��ͼ2��ʾ��
�ɣ�1��֪����A1C1B�ա�ACB��
��A1B=AB��BC1=BC����A1BC1=��ABC��
���1=��2�� ![]() =
= ![]() =
= ![]() ��
��
���A1BA�ס�C1BC��
�� ![]() =��
=�� ![]() ��2��
��2��
�ߡ�CBC1�����Ϊ16��
���ABA1�����=9
��3��
��ͼ3��ʾ����P��AC���˶�����C����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1���
���ֵΪ��EP1=BC+BE=8+3=11��
���߶�EP1���ȵ����ֵΪ11��
����������1������ת�����ʿɵã���A1C1B=��ACB=30�㣬BC=BC1 �� ���ɵ��������ε����ʣ�������á�CC1A1�Ķ�������2�����ɡ�ABC�ա�A1BC1 �� ��֤�á�ABA1�ס�CBC1 �� Ȼ���������������ε�����ȵ������Ʊȵ�ƽ����������á�ABA1��������ڵ�P��AC���˶�����C����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1���������߶�EP1���ȵ����ֵ��
�����㾫�����������������ε��ж�����ת�����ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���������ε��ж�����:���Ƕ�Ӧ��ȣ������������ƣ�ASA����ֱ�������α�б���ϵĸ߷ֳɵ�����ֱ�������κ�ԭ���������ƣ� ���߶�Ӧ�ɱ����Ҽн���ȣ������������ƣ�SAS�������߶�Ӧ�ɱ����������������ƣ�SSS��������ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��ˣ�


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�����عˣ���ѧϰ��������λ��ʱ��Ϊ��̽����������λ�ߵ����ʣ�˼·���£�
��һ�����Ӹ����ߣ���ͼ1����![]() �У��ӳ�
�У��ӳ�![]() ��
��![]() �ֱ���
�ֱ���![]() ���е㣩����
���е㣩����![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��
�ڶ���֤��![]() ����֤�ı���
����֤�ı���![]() ��ƽ���ı��Σ��Ӷ��ó���������λ�ߵ����ʽ��ۣ�____________________________________������DE��BC��ʾ��
��ƽ���ı��Σ��Ӷ��ó���������λ�ߵ����ʽ��ۣ�____________________________________������DE��BC��ʾ��
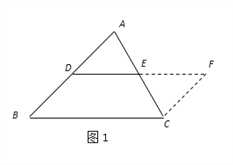
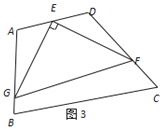
��2������������ͼ2����������ABCD�У�EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG��2��DF��3����GEF��90�㣬��GF�ij���

��3����չ�о�����ͼ3�����ı���ABCD�У���A��105�㣬��D��120�㣬EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG��![]() ��DF��2����GEF��90�㣬��GF�ij���
��DF��2����GEF��90�㣬��GF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ѧС���������Ȼ�У�������������100ƪ�����������ȵķ���������Ϊ�������������黭��Ƶ���ֲ�ֱ��ͼ����ͼ������֪������5��С�����εĸߵı�Ϊl��3��7��6��3����ô����������б���Ϊ��������ģ��������ڻ����80��Ϊ���㣩��____ƪ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��E��F�ֱ�����������ABC�������ϣ��ҡ�DEFҲ���������Σ�����ABC�ı߳�Ϊa����DEF�ı߳�Ϊb�����AEF������Բ�뾶Ϊ �� 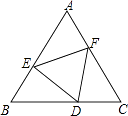
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
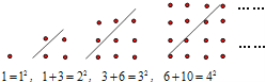
����Ŀ����ϣ�������ıϴ����˹ѧ�ɰ�1��3��6��10 ������������Ϊ������������������1��4��9��16 ������������Ϊ������������������ͼ�п��Է��֣��κ�һ������1�������������������Կ�����������������������֮�ͣ��õ�ʽ��ʾ��100�������ε����еĹ���_________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ֻ����ռ�����![]() һ����������
һ����������![]() ������������ץס���ֻ��ᣬ���������������ܶ�ũ��ƷҲ�ı���ԭ��������ģʽ��ʵ�����������ۣ��ⲻ�մ�ѧ��ҵ��С�����ԼҵĶ����ƷҲ�ŵ������ϣ���ԭ�ƻ�ÿ����100�ﶬ�棬����������ԭ��ʵ��ÿ�����������ƻ�������г��룬�±���ij�ܵ��������
������������ץס���ֻ��ᣬ���������������ܶ�ũ��ƷҲ�ı���ԭ��������ģʽ��ʵ�����������ۣ��ⲻ�մ�ѧ��ҵ��С�����ԼҵĶ����ƷҲ�ŵ������ϣ���ԭ�ƻ�ÿ����100�ﶬ�棬����������ԭ��ʵ��ÿ�����������ƻ�������г��룬�±���ij�ܵ��������![]() �����Ϊ���������Ϊ��
����������������![]() �����
�����![]() ��
��
���� | һ | �� | �� | �� | �� | �� | �� |
��ƻ����IJ�ֵ |
|
|
|
|
|
|
|
(1)���ݼ�¼�����ݿ�֪ǰ���칲���� ______ �
(2)���ݼ�¼�����ݿ�֪����������һ������������ٵ�һ������� ______ �
(3)����ʵ�����������ﵽ�˼ƻ�����û�У�
(4)������ÿ�ﰴ8Ԫ���ۣ�ÿ�ﶬ����˷�ƽ��3Ԫ����ôС������һ���������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���BAC=90�㣬D��BC�е㣬E��AD�е㣬��A��AF��BC

����֤����AEF�ա�DEB��
����֤���ı���ADCF�����Σ�
����AB=5��AC=4��������ADCF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��a��b��c�������ϵ�λ����ͼ��ʾ����
��1��������������������գ�a____0��b____0��c_____0��
��2��������������������գ���a____0��a��b____0��c��a____0��
��3������|��a|��|a��b|+|c��a|
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��ͼ����A����2��0������B��4��0������D��2��4������y�ύ�ڵ�C����ֱ��BC������AC��CD�� 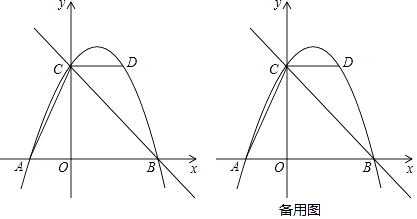
��1���������ߵĺ�������ʽ��
��2��E���������ϵĵ㣬�������ECD=��ACO�ĵ�E�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com