
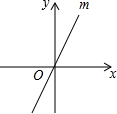
 如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).
如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2). 分析 由题意可知点N的纵坐标为2或-2,当N在x轴上方时,过N作x轴的垂直交直线于点M,交x轴于点F,过N作NE⊥直线m,垂足为E,当N在直线m下方时则有∠OMN=30°,当N在直线m上方时则有∠NME=30°,利用直角三角形的性质可求得点N的横坐标,再根据对称性可求得N在x轴下方时的坐标,可得出答案.
解答 解:∵N到x轴的距离为2,
∴N点纵坐标为2或-2,
当N点在x轴上方时,分两种情况:
①当N在直线m下方时,
如图1,过N作NF⊥x轴于点F,交直线m于点M,过N作NE⊥直线m,垂足为E,则NE=1,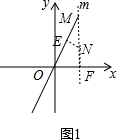
∵∠MOF=60°,
∴∠OMF=30°,
在Rt△MEN中,MN=2NE=2,
∴MF=2+2=4,
∴OF=FMtan30°=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴此时N点坐标为($\frac{4\sqrt{3}}{3}$,2);
②当N点在直线m上方时,如图2,过N作NE⊥直线m于点E,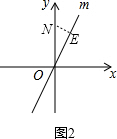
则NE=1,且直线m与y轴的夹角为30°,
∵N到x轴的距离为2,
∴N点在y轴上,
∴此时N点坐标为(0,2);
当N点在x轴下方时,由对称性可知N点的坐标为($\frac{4\sqrt{3}}{3}$,-2)或(0,-2);
综上可知N点的坐标为:(0,2)或(0,-2)或($\frac{4}{3}\sqrt{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).
故答案为:(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).
点评 本题主要考查一次函数图象点的坐标和直角三角形的性质,根据条件确定出N点的位置是解题的关键,注意分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
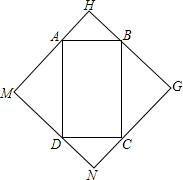 近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米.
近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
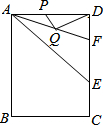 已知,在矩形ABCD中,AD=6,AB=8,∠BAD的平分线交DC于点E,∠DAF=22.5°,若点P、Q分别是AD、AF上的动点,则DQ+PQ的最小值为3$\sqrt{2}$.
已知,在矩形ABCD中,AD=6,AB=8,∠BAD的平分线交DC于点E,∠DAF=22.5°,若点P、Q分别是AD、AF上的动点,则DQ+PQ的最小值为3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 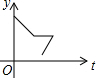 | B. | 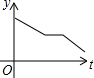 | C. | 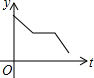 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为(1,3)或(5,1).
如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为(1,3)或(5,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
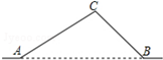 如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com