
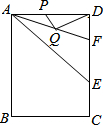
 已知,在矩形ABCD中,AD=6,AB=8,∠BAD的平分线交DC于点E,∠DAF=22.5°,若点P、Q分别是AD、AF上的动点,则DQ+PQ的最小值为3$\sqrt{2}$.
已知,在矩形ABCD中,AD=6,AB=8,∠BAD的平分线交DC于点E,∠DAF=22.5°,若点P、Q分别是AD、AF上的动点,则DQ+PQ的最小值为3$\sqrt{2}$. 分析 首先在AE上取点M,使得AM=AP,作DN⊥AE于点N,然后根据全等三角形判定的方法,判断出△APQ≌△AMQ,即可判断出DQ+PQ=DM;最后根据DN⊥AE,求出DN的值,即可判断出DQ+PQ的最小值,据此解答即可.
解答 解:如图1,在AE上取点M,使得AM=AP,作DN⊥AE于点N,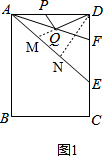 ,
,
∵AE是∠BAD的平分线,
∴∠DAE=90°÷2=45°,
∵∠DAF=22.5°,
∴∠EAF=45°-22.5°=22.5°,
∴∠DAF=∠EAF,
在△APQ和△AMQ中,
$\left\{\begin{array}{l}{AP=AM}\\{∠PAQ=∠MAQ}\\{AQ=AQ}\end{array}\right.$,
∴△APQ≌△AMQ,
∴PQ=MQ,
∴DQ+PQ=DQ+MQ=DM,
∵DN⊥AE,DN=AD×sin45°=6×$\frac{\sqrt{2}}{2}$=3$\sqrt{2}$,
∴DQ+PQ的最小值为3$\sqrt{2}$.
故答案为:$3\sqrt{2}$.
点评 (1)此题主要考查了轴对称-最短路线问题,要熟练掌握,解答此题的关键是要明确:凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.
(2)此题还考查了矩形的性质和应用,要熟练掌握,解答此题的关键是要明确:①平行四边形的性质矩形都具有;②角:矩形的四个角都是直角;③边:邻边垂直;④对角线:矩形的对角线相等;⑤矩形是轴对称图形,又是中心对称图形.它有2条对称轴,分别是每组对边中点连线所在的直线;对称中心是两条对角线的交点.


科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
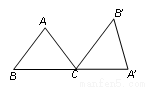
如图,在△ABC中,AB=AC =5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C,若点A′恰好落在BC的延长线上,则点B′到BA′的距离为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
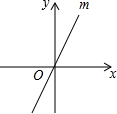 如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).
如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
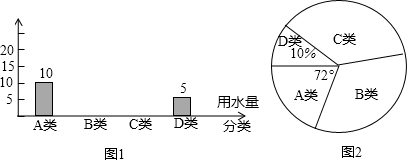
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
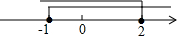 把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{x>-1}\\{x≤2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥-1}\\{x<2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥-1}\\{x≤2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<-1}\\{x≥2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
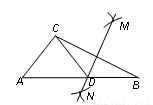
如图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于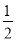 BC的长为半径作弧,两弧交于M,N两点;②作直线MN交AB于点D,连接CD.如果已知CD=AC,∠B=25°,则∠ACB的度数为__________.
BC的长为半径作弧,两弧交于M,N两点;②作直线MN交AB于点D,连接CD.如果已知CD=AC,∠B=25°,则∠ACB的度数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com