
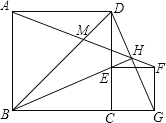
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
【答案】①②③④
【解析】
①由已知条件可证得△BEC≌△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90°,所以∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;②若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45°,所以②的结论也是正确的.③此题要通过相似三角形来解;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;④若BE平分∠DBC,那么H是DG的中点;易证得△ABH∽△BCE,得BDBC=BEBH,即![]() BC2=BEBH,因此只需求出BEBH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BEBH的值,由此得解.
BC2=BEBH,因此只需求出BEBH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BEBH的值,由此得解.
解:①正确,证明如下:
∵BC=DC,CE=CG,∠BCE=∠DCG=90°,
∴△BEC≌△DGC,∴∠EBC=∠CDG,
∵∠BDC+∠DBH+∠EBC=90°,
∴∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;
②由于∠BAD、∠BCD、∠BHD都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;
由圆周角定理知:∠DHA=∠ABD=45°,故②正确;
③由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH;
又∵∠ABD=∠DBG=45°,
∴△ABM∽△DBG,得AM:DG=AB:BD=1:![]() ,即DG=
,即DG=![]() AM;
AM;
故③正确;
④过H作HN⊥CD于N,连接EG;

若BH平分∠DBG,且BH⊥DG,已知:BH垂直平分DG;
得DE=EG,H是DG中点,HN为△DCG的中位线;
设CG=x,则:HN=![]() x,EG=DE=
x,EG=DE=![]() x,DC=BC=(
x,DC=BC=(![]() +1)x;
+1)x;
∵HN⊥CD,BC⊥CD,
∴HN∥BC,
∴∠NHB=∠EBC,∠ENH=∠ECB,
∴△BEC∽△HEN,则BE:EH=BC:HN=2![]() +2,即EH=
+2,即EH=![]() ;
;
∴HEBH=BH![]() =4-2
=4-2![]() ,即BEBH=4
,即BEBH=4![]() ;
;
∵∠DBH=∠CBE,且∠BHD=∠BCE=90°,
∴△span>DBH∽△EBC,得:DBBC=BEBH=4![]() ,
,
即![]() BC2=4
BC2=4![]() ,得:BC2=4,即正方形ABCD的面积为4;
,得:BC2=4,即正方形ABCD的面积为4;
故④正确;
故答案为:①②③④.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到![]() 、
、![]() 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往
两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往![]() 、
、![]() 两城镇的运费分别为每辆800元和900元,用小货车运往
两城镇的运费分别为每辆800元和900元,用小货车运往![]() 、
、![]() 两城镇的运费分别为每辆400元和600元.
两城镇的运费分别为每辆400元和600元.
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往![]() 城镇,其余货车前往
城镇,其余货车前往![]() 城镇,设前往
城镇,设前往![]() 城镇的大货车为
城镇的大货车为![]() 辆,前往
辆,前往![]() 、
、![]() 两城镇总费用为
两城镇总费用为![]() 元,试求出
元,试求出![]() 与
与![]() 的函数解析式.若运往
的函数解析式.若运往![]() 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
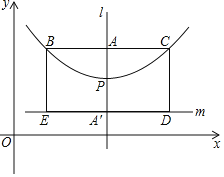
【题目】如图,在顶点为P的抛物线y=a(x-h)2+k(a≠0)的对称轴1的直线上取点A(h,k+![]() ),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
(1)直接写出抛物线y=![]() x2的焦点坐标以及直径的长.
x2的焦点坐标以及直径的长.
(2)求抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点坐标以及直径的长.
的焦点坐标以及直径的长.
(3)已知抛物线y=a(x-h)2+k(a≠0)的直径为![]() ,求a的值.
,求a的值.
(4)①已知抛物线y=a(x-h)2+k(a≠0)的焦点矩形的面积为2,求a的值.
②直接写出抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
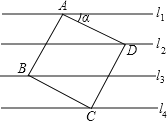
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
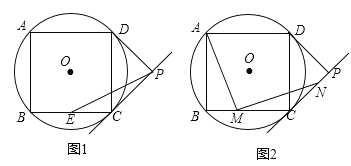
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时, y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人从A城出发,前往距离A城30千米的B城.现在有三种方案供他选择:
①骑自行车,其速度为15千米/时;
②蹬三轮车,其速度为10千米/时;
③骑摩托车,其速度为40千米/时.
(1)选择哪种方式能使他从A城到达B城的时间不超过2小时?请说明理由;
(2)设此人在行进途中离B城的距离为s(千米),行进时间为t(时),就(1)所选定的方案,试写出s与t之间的函数关系式(注明自变量t的取值范围),并在如图所示的平面直角坐标系中画出函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
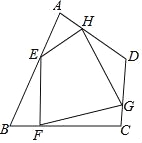
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com