
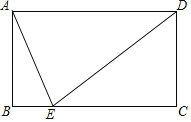
【题目】如图,已知矩形ABCD中,BC=2AB,点E在BC边上,连接DE、AE,若EA平分∠BED,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过点A作AF⊥DE于F,根据角平分线上的点到角的两边距离相等可得AF=AB,利用全等三角形的判定和性质以及矩形的性质解答即可.
解:如图,过点A作AF⊥DE于F,
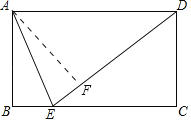
在矩形ABCD中,AB=CD,
∵AE平分∠BED,
∴AF=AB,
∵BC=2AB,
∴BC=2AF,
∴∠ADF=30°,
在△AFD与△DCE中
∵∠C=∠AFD=90°,
∠ADF=∠DEC,
AF=DC,,
∴△AFD≌△DCE(AAS),
∴△CDE的面积=△AFD的面积=![]()
∵矩形ABCD的面积=ABBC=2AB2,
∴2△ABE的面积=矩形ABCD的面积﹣2△CDE的面积=(2﹣![]() )AB2,
)AB2,
∴△ABE的面积=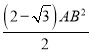 ,
,
∴ ,
,
故选:C.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某口罩加工厂有![]() 两组工人共
两组工人共![]() 人,
人,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 两组工人每小时一共可加工口罩
两组工人每小时一共可加工口罩![]() 只.
只.
(1)求![]() 两组工人各多少人;
两组工人各多少人;
(2)由于疫情加重![]() 两组工人均提高了工作效率,一名
两组工人均提高了工作效率,一名![]() 组工人和一名
组工人和一名![]() 组工人每小时共可生产口罩
组工人每小时共可生产口罩![]() 只,若
只,若![]() 两组工人每小时至少加工
两组工人每小时至少加工![]() 只口罩,那么
只口罩,那么![]() 组工人每人每小时至少加工多少只口罩?
组工人每人每小时至少加工多少只口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现:如图①,点A为一动点,点B和点C为两个定点,且![]() ,
,![]() (
(![]() ).
).
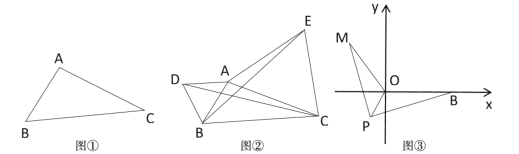
填空:当点![]() 位于_______时,线段
位于_______时,线段![]() 的长取得最小值,且最小值为_______(用含
的长取得最小值,且最小值为_______(用含![]() 的式子表示);
的式子表示);
(2)如图②应用:点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,如图2分别以
,如图2分别以![]() 、
、![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 、
、![]() .
.
①请找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最小值.
长的最小值.
(3)拓展:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段OB外一动点,且
为线段OB外一动点,且![]() ,
,![]() ,
,![]() ,请求出
,请求出![]() 的最小值并直接写出点
的最小值并直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
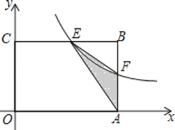
(1)当F为AB的中点时,求该反比例函数的解析式和点E的坐标.
(2)设过(1)中的直线EF的解析式为y=ax+b,直接写出不等式ax+b<![]() 的解集.
的解集.
(3)当k为何值时,△AEF的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
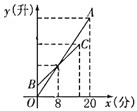
【题目】一个蓄水池有甲、乙两个注水管和一个排水管丙,三个水管均已关闭,已知乙注水管的注水速度为10升/分.先打开乙注水管4分钟,再打开甲注水管,甲、乙两个水管均注水20分钟.设甲注水管的工作时间为![]() (分),甲注水管的注水量
(分),甲注水管的注水量![]() (升)与时间
(升)与时间![]() (分)的函数图象为线段
(分)的函数图象为线段![]() ,乙注水管的注水量
,乙注水管的注水量![]() (升)与时间
(升)与时间![]() (分)的函数图象为线段
(分)的函数图象为线段![]() ,如图所示.
,如图所示.
(1)求甲注水管的总注水量;
(2)求线段![]() 所对应的函数关系式,并写出自变量的取值范围;
所对应的函数关系式,并写出自变量的取值范围;
(3)乙注水管打开的16分钟后,打开丙出水管.已知出水管丙的排水速度为20升/分,求丙出水管打开多长时间能将蓄水池的水排空.
查看答案和解析>>
科目:初中数学 来源: 题型:
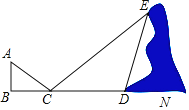
【题目】如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开的桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上的数据求出DE的长度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
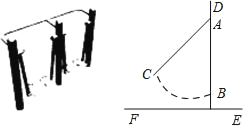
【题目】图1中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看图2,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°,求此时点C距离地面EF的高度.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
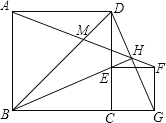
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是平行四边形ABCD边上的点,AP=![]() AB,射线CP交DA的延长线于点E,则S△APE:S平行四边形ABCD等于( )
AB,射线CP交DA的延长线于点E,则S△APE:S平行四边形ABCD等于( )

A. 1:5B. 1:8C. 1:12D. 1:13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com