
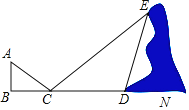
����Ŀ����ͼ��С����ͬ���ڴ����ڼ䣬������ij��Сɽ�µĵ�E����һ��ʢ�����һ���С��������������ƽ�澵�����ķ�ʽ����һ��С������ɽ���µľ��룬��DE�ij��ȣ�С��վ�ڵ�B��λ�ã���ͬ���ƶ�ƽ�澵����C������ʱС����ƽ�澵�ڿ��Կ�����E����BC��2.7�ף�CD��11.5�ף���CDE��120�㣬��֪С��������Ϊ1.8�ף������������ϵ��������DE�ij��ȣ�������������ţ�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
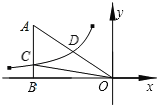
����Ŀ����ͼ����֪˫����![]() ��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����6��4�������AOC�����Ϊ_____��
��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����6��4�������AOC�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��
��![]() �ύ�ڵ�A����y�ύ�ڵ�C������ACBE�Ķ���B�ڵ�һ���ķ���������
�ύ�ڵ�A����y�ύ�ڵ�C������ACBE�Ķ���B�ڵ�һ���ķ���������![]() ͼ���ϣ�����B��
ͼ���ϣ�����B��![]()
![]() ������ΪF����OF=t��
������ΪF����OF=t��
��1�����ACO������ֵ��
��2�����B�����꣨�ú�t��ʽ�ӱ�ʾ����
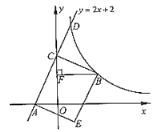
��3����ֱ֪��![]() �뷴��������
�뷴��������![]() ͼ������һ���ĵ�D������DE�����
ͼ������һ���ĵ�D������DE�����![]() �ᣬ��m��ֵ��
�ᣬ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ��һ�㣬
��һ�㣬![]() ƽ��
ƽ��![]() ��
��![]() ��
��
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ����
����![]() �ij���Ϊ ��
�ij���Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
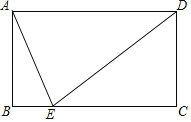
����Ŀ����ͼ����֪����ABCD�У�BC��2AB����E��BC���ϣ�����DE��AE����EAƽ�֡�BED����![]() ��ֵΪ��������
��ֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() ��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
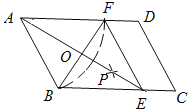
��1���ı���ABEF��_______����ѡ����Ρ����Ρ������Ρ���ȷ������ֱ����д�����
��2��AE��BF�ཻ�ڵ�O�����ı���ABEF���ܳ�Ϊ40��BF=10����AE�ij�Ϊ________����ABC=________������ֱ����д�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
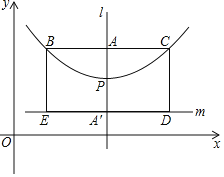
����Ŀ����ͼ���ڶ���ΪP��������y=a��x-h��2+k��a��0���ĶԳ���1��ֱ����ȡ��A��h��k+![]() ������A��BC��l����������B��C���㣨B��C����ࣩ����͵�A���ڵ�P�Գƣ���A��ֱ��m��l���ֱַ����B��C��ֱ��BE��m��CD��m������ΪE��D����������ǰѵ�A�д������ߵĽ��㣬BC�д������ߵ�ֱ��������BCDE�д������ߵĽ�����Σ�
������A��BC��l����������B��C���㣨B��C����ࣩ����͵�A���ڵ�P�Գƣ���A��ֱ��m��l���ֱַ����B��C��ֱ��BE��m��CD��m������ΪE��D����������ǰѵ�A�д������ߵĽ��㣬BC�д������ߵ�ֱ��������BCDE�д������ߵĽ�����Σ�
��1��ֱ��д��������y=![]() x2�Ľ��������Լ�ֱ���ij���
x2�Ľ��������Լ�ֱ���ij���
��2����������y=![]() x2-
x2-![]() x+
x+![]() �Ľ��������Լ�ֱ���ij���
�Ľ��������Լ�ֱ���ij���
��3����֪������y=a��x-h��2+k��a��0����ֱ��Ϊ![]() ����a��ֵ��
����a��ֵ��
��4������֪������y=a��x-h��2+k��a��0���Ľ�����ε����Ϊ2����a��ֵ��
��ֱ��д��������y=![]() x2-
x2-![]() x+
x+![]() �Ľ��������������y=x2-2mx+m2+1����������ֱ���1���Լ�2��ʱm��ֵ��
�Ľ��������������y=x2-2mx+m2+1����������ֱ���1���Լ�2��ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
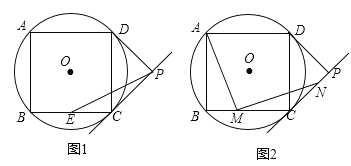
����Ŀ����ͼ���ı���ABCD�ǡ�O���ڽ������Σ�AB=4��PC��PD�ǡ�O���������ߣ�C��DΪ�е㣮
��1����ͼ1�����O�İ뾶��
��2����ͼ1������E��BC���е㣬����PE����PE�ij��ȣ�
��3����ͼ2������M��BC��������һ�㣨����B��C�����Ե�MΪֱ�Ƕ��㣬��BC���Ϸ�����AMN=90������ֱ��CP�ڵ�N����֤��AM=MN��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
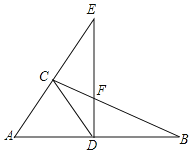
����Ŀ����֪����ͼ����Rt��ABC�У�CD��б���ϵ����ߣ�DE��AB��BC�ڵ�F����AC���ӳ����ڵ�E��
��֤����1����ADE�ס�FDB��
��2��CD2=DEDF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com