
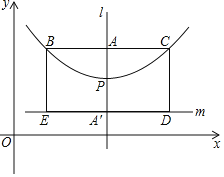
【题目】如图,在顶点为P的抛物线y=a(x-h)2+k(a≠0)的对称轴1的直线上取点A(h,k+![]() ),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
(1)直接写出抛物线y=![]() x2的焦点坐标以及直径的长.
x2的焦点坐标以及直径的长.
(2)求抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点坐标以及直径的长.
的焦点坐标以及直径的长.
(3)已知抛物线y=a(x-h)2+k(a≠0)的直径为![]() ,求a的值.
,求a的值.
(4)①已知抛物线y=a(x-h)2+k(a≠0)的焦点矩形的面积为2,求a的值.
②直接写出抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
【答案】(1)4(2)4(3)![]() (4)①a=±
(4)①a=±![]() ;②当m=1-
;②当m=1-![]() 或m=5+
或m=5+![]() 时,1个公共点,当1-
时,1个公共点,当1-![]() <m≤1或5≤m<5+
<m≤1或5≤m<5+![]() 时,2个公共点,
时,2个公共点,
【解析】
(1)根据题意可以求得抛物线y=![]() x2的焦点坐标以及直径的长;
x2的焦点坐标以及直径的长;
(2)根据题意可以求得抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点坐标以及直径的长;
的焦点坐标以及直径的长;
(3)根据题意和y=a(x-h)2+k(a≠0)的直径为![]() ,可以求得a的值;
,可以求得a的值;
(4)①根据题意和抛物线y=ax2+bx+c(a≠0)的焦点矩形的面积为2,可以求得a的值;
②根据(2)中的结果和图形可以求得抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点矩形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
的焦点矩形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
(1)∵抛物线y=![]() x2,
x2,
∴此抛物线焦点的横坐标是0,纵坐标是:0+![]() =1,
=1,
∴抛物线y=![]() x2的焦点坐标为(0,1),
x2的焦点坐标为(0,1),
将y=1代入y=![]() x2,得x1=-2,x2=2,
x2,得x1=-2,x2=2,
∴此抛物线的直径是:2-(-2)=4;
(2)∵y=![]() x2-
x2-![]() x+
x+![]() =
=![]() (x-3)2+2,
(x-3)2+2,
∴此抛物线的焦点的横坐标是:3,纵坐标是:2+![]() =3,
=3,
∴焦点坐标为(3,3),
将y=3代入y=![]() (x-3)2+2,得
(x-3)2+2,得
3=![]() (x-3)2+2,解得,x1=5,x2=1,
(x-3)2+2,解得,x1=5,x2=1,
∴此抛物线的直径时5-1=4;
(3)∵焦点A(h,k+![]() ),
),
∴k+![]() =a(x-h)2+k,解得,x1=h+
=a(x-h)2+k,解得,x1=h+![]() ,x2=h-
,x2=h-![]() ,
,
∴直径为:h+![]() -(h-
-(h-![]() )=
)=![]() =
=![]() ,
,
解得,a=±![]() ,
,
即a的值是![]() ;
;
(4)①由(3)得,BC=![]() ,
,
又CD=A'A=![]() .
.
所以,S=BCCD=![]()
![]() =
=![]() =2.
=2.
解得,a=±![]() ;
;
②当m=1-![]() 或m=5+
或m=5+![]() 时,1个公共点,当1-
时,1个公共点,当1-![]() <m≤1或5≤m<5+
<m≤1或5≤m<5+![]() 时,2个公共点,
时,2个公共点,
理由:由(2)知抛,物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点矩形顶点坐标分别为:
的焦点矩形顶点坐标分别为:
B(1,3),C(5,3),E(1,1),D(5,1),
当y=x2-2mx+m2+1=(x-m)2+1过B(1,3)时,m=1-![]() 或m=1+
或m=1+![]() (舍去),过C(5,3)时,m=5-
(舍去),过C(5,3)时,m=5-![]() (舍去)或m=5+
(舍去)或m=5+![]() ,
,
∴当m=1-![]() 或m=5+
或m=5+![]() 时,1个公共点;
时,1个公共点;
当1-![]() <m≤1或5≤m<5+
<m≤1或5≤m<5+![]() 时,2个公共点.
时,2个公共点.
由图可知,公共点个数随m的变化关系为
当m<1-![]() 时,无公共点;
时,无公共点;
当m=1-![]() 时,1个公共点;
时,1个公共点;
当1-![]() <m≤1时,2个公共点;
<m≤1时,2个公共点;
当1<m<5时,3个公共点;
当5≤m<5+![]() 时,2个公共点;
时,2个公共点;
当m=5+![]() 时,1个公共点;
时,1个公共点;
当m>5+![]() 时,无公共点;
时,无公共点;
由上可得,当m=1-![]() 或m=5+
或m=5+![]() 时,1个公共点;
时,1个公共点;
当1-![]() <m≤1或5≤m<5+
<m≤1或5≤m<5+![]() 时,2个公共点.
时,2个公共点.


科目:初中数学 来源: 题型:
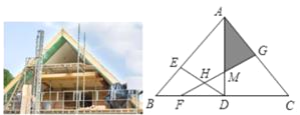
【题目】工人师傅在修茸一人字架屋顶BAC时需要加固,计划焊接三根钢条AD,DE,FG.在如图所示的△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E,F,G分别是AB,BD,AC上的点,连接DE,GF,交于点H,GF与AD交于点M,当H为FM的中点,BF∶CF=1∶5,AG:AE=5:7时,△AGM的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
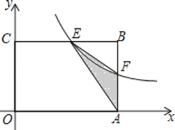
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该反比例函数的解析式和点E的坐标.
(2)设过(1)中的直线EF的解析式为y=ax+b,直接写出不等式ax+b<![]() 的解集.
的解集.
(3)当k为何值时,△AEF的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
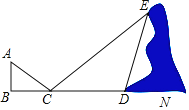
【题目】如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开的桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上的数据求出DE的长度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
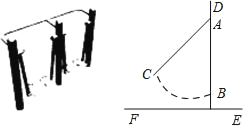
【题目】图1中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看图2,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°,求此时点C距离地面EF的高度.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x-c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
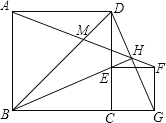
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资![]() (吨)与时间
(吨)与时间![]() (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
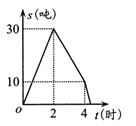
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com