
【题目】(1)发现:如图①,点A为一动点,点B和点C为两个定点,且![]() ,
,![]() (
(![]() ).
).
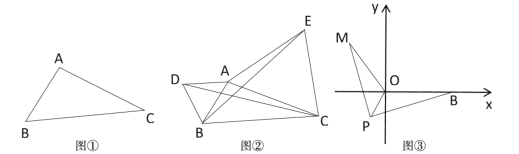
填空:当点![]() 位于_______时,线段
位于_______时,线段![]() 的长取得最小值,且最小值为_______(用含
的长取得最小值,且最小值为_______(用含![]() 的式子表示);
的式子表示);
(2)如图②应用:点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,如图2分别以
,如图2分别以![]() 、
、![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 、
、![]() .
.
①请找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最小值.
长的最小值.
(3)拓展:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段OB外一动点,且
为线段OB外一动点,且![]() ,
,![]() ,
,![]() ,请求出
,请求出![]() 的最小值并直接写出点
的最小值并直接写出点![]() 的坐标.
的坐标.
【答案】(1)线段BC上,![]() ;(2)①
;(2)①![]() ,理由见解析;②
,理由见解析;②![]() ;(3)
;(3)![]()
【解析】
(1)直接根据三角形三边关系即可得出答案;
(2)①首先根据等边三角形的性质得出![]() ,然后由全等三角形的性质即可得出答案;
,然后由全等三角形的性质即可得出答案;
②线段BE长度的最小值=线段CD长度的最小值,当点D在BC边上时,CD最小,即可求出答案;
(3)在y轴上取点![]() ,连接
,连接![]() ,在点P所在的圆O上取一点
,在点P所在的圆O上取一点![]() ,连接
,连接![]() ,依题意作
,依题意作![]() ,使
,使![]() ,连接
,连接![]() ,首先利用相似三角形的性质得出点M在以
,首先利用相似三角形的性质得出点M在以![]() 为圆心的圆上运动,
为圆心的圆上运动,![]() ,从而可求出OM的最小值,此时M在y轴上,通过全等三角形的性质得出
,从而可求出OM的最小值,此时M在y轴上,通过全等三角形的性质得出![]() ,然后设
,然后设![]() ,建立方程组即可求出此时P点的坐标.
,建立方程组即可求出此时P点的坐标.
(1)![]() ,
,![]() ,
,![]() ,
,
∴当点A位于线段BC上时,线段AC的长取得最小值,且最小值为![]() ;
;
(2)①![]() ,理由如下:
,理由如下:
∵![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,
![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,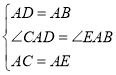
![]() ,
,
![]() ;
;
②当点D在BC边上时,CD最小,此时 ![]() ,
,
∵![]() ,
,
∴线段![]() 长的最小值为
长的最小值为![]() ;
;
(3)在y轴上取点![]() ,连接
,连接![]() ,在点P所在的圆O上取一点
,在点P所在的圆O上取一点![]() ,连接
,连接![]() ,依题意作
,依题意作![]() ,使
,使![]() ,连接
,连接![]() ,
,
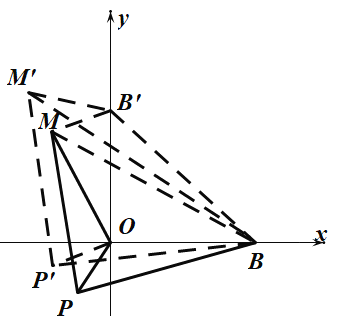
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
同理,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴点M在以![]() 为圆心的圆上运动,
为圆心的圆上运动,![]() ,
,
∴OM的最小值为![]() .
.
如图,此时M点在y轴上,设此时P点为![]() ,过点
,过点![]() 作
作![]() 轴于点E,延长
轴于点E,延长![]() ,过点B作
,过点B作![]() 于点F,
于点F,

∵![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,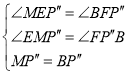
![]() ,
,
![]() .
.
设![]() ,
,
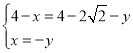 解得
解得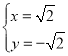
∴此时P的坐标为![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.
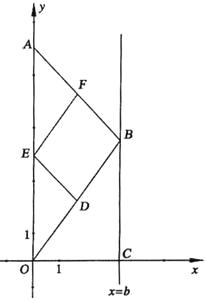
(1)判断四边形DEFB的形状.并证明你的结论;
(2)试求四边形DEFB的面积S与b的关系式;
(3)设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
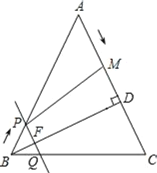
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM=S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到![]() 、
、![]() 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往
两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往![]() 、
、![]() 两城镇的运费分别为每辆800元和900元,用小货车运往
两城镇的运费分别为每辆800元和900元,用小货车运往![]() 、
、![]() 两城镇的运费分别为每辆400元和600元.
两城镇的运费分别为每辆400元和600元.
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往![]() 城镇,其余货车前往
城镇,其余货车前往![]() 城镇,设前往
城镇,设前往![]() 城镇的大货车为
城镇的大货车为![]() 辆,前往
辆,前往![]() 、
、![]() 两城镇总费用为
两城镇总费用为![]() 元,试求出
元,试求出![]() 与
与![]() 的函数解析式.若运往
的函数解析式.若运往![]() 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点![]() 的横坐标,第二个数作为点
的横坐标,第二个数作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 在反比例函数
在反比例函数![]() 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数![]() 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点![]() 的情形;
的情形;
(2)分别求出点![]() 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴交于点A,与y轴交于点C,矩形ACBE的顶点B在第一象限的反比例函数
轴交于点A,与y轴交于点C,矩形ACBE的顶点B在第一象限的反比例函数![]() 图像上,过点B作
图像上,过点B作![]()
![]() ,垂足为F,设OF=t.
,垂足为F,设OF=t.
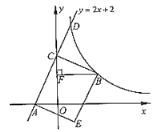
(1)求∠ACO的正切值;
(2)求点B的坐标(用含t的式子表示);
(3)已知直线![]() 与反比例函数
与反比例函数![]() 图像都经过第一象限的点D,联结DE,如果
图像都经过第一象限的点D,联结DE,如果![]() 轴,求m的值.
轴,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时, y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com