
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
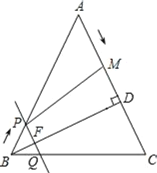
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM=S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
【答案】(1)当t=![]() 时,四边形PQCM是平行四边形;(2)y=
时,四边形PQCM是平行四边形;(2)y=![]() t2﹣8t+40;(3)不存在;详见解析;(4)t=
t2﹣8t+40;(3)不存在;详见解析;(4)t=![]() s时,点M在线段PC的垂直平分线上.
s时,点M在线段PC的垂直平分线上.
【解析】
(1)假设PQCM为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
(2)根据PQ∥AC,利用相似三角形的性质可得三角形BPQ也为等腰三角形,即BP=PQ=t,用含t的代数式就可以表示出BF,进而得到梯形的高DF=![]() 又点M的运动速度和时间可知点M走过的路程AM=2t,所以梯形的下底CM=10-2t.最后根据梯形的面积公式即可得到y与t的关系式;
又点M的运动速度和时间可知点M走过的路程AM=2t,所以梯形的下底CM=10-2t.最后根据梯形的面积公式即可得到y与t的关系式;
(3)根据三角形的面积公式,先求出三角形ABC的面积,又根据S四边形PQCM=S△ABC,求出四边形PQCM的面积,从而得到了y的值,代入第二问求出的y与t的解析式中求出t的值即可;
(4)假设存在,则根据垂直平分线上的点到线段两端点的距离相等即可得到MP=MC,过点M作MH垂直AB,由一对公共角的相等和一对直角的相等即可得到△AHM∽△ADB,由相似得到对应边成比例进而用含t的代数式表示出AH和HM的长,再由AP的长减AH的长表示出PH的长,从而在直角三角形PHM中根据勾股定理表示出MP的平方,再由AC的长减AM的长表示出MC的平方,根据两者的相等列出关于t的方程进而求出t的值.
解:(1)假设四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10﹣t=2t,
解得:![]()
∴当![]() 时,四边形PQCM是平行四边形;
时,四边形PQCM是平行四边形;
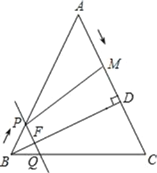
(2)∵PQ∥AC,
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴![]() 即
即![]()
解得:![]()
∴FD=BD﹣BF=8﹣![]() ,
,
又∵MC=AC﹣AM=10﹣2t,
∴y=![]() (PQ+MC)FD=
(PQ+MC)FD=![]()
(3)不存在;
∵S△ABC=![]()
当S![]()
解得:t=0,或t=20,都不合题意,因此不存在;
(4)假设存在某一时刻t,使得M在线段PC的垂直平分线上,则MP=MC,
过M作MH⊥AB,交AB与H,如图所示:
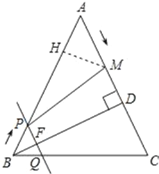
∵∠A=∠A,∠AHM=∠ADB=90°,
∴△AHM∽△ADB,
∴![]()
又∵AD=![]()
∴![]()
∴![]()
∴HP=10﹣t﹣![]() =10﹣
=10﹣![]()
在Rt△HMP中,![]()
又∵MC2=![]() =100﹣40t+4t2,
=100﹣40t+4t2,
∵MP2=MC2,
∴![]()
解得![]() (舍去),
(舍去),
∴![]() 时,点M在线段PC的垂直平分线上.
时,点M在线段PC的垂直平分线上.


科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在画有方格图的平面直角坐标系中,△ABC的三个顶点均在格点上.
(1)将△ACB绕点B顺时针方向旋转![]() ,在方格图中用直尺画出旋转后对应的△A1C1B,则A1点的坐标是(_________),C1点的坐标是(_________).
,在方格图中用直尺画出旋转后对应的△A1C1B,则A1点的坐标是(_________),C1点的坐标是(_________).
(2)在方格图中用直尺画出△ACB关于原点O的中心对称图形△A2C2B2,则A2点的坐标是(_________),C2点的坐标是(_________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某口罩加工厂有![]() 两组工人共
两组工人共![]() 人,
人,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 两组工人每小时一共可加工口罩
两组工人每小时一共可加工口罩![]() 只.
只.
(1)求![]() 两组工人各多少人;
两组工人各多少人;
(2)由于疫情加重![]() 两组工人均提高了工作效率,一名
两组工人均提高了工作效率,一名![]() 组工人和一名
组工人和一名![]() 组工人每小时共可生产口罩
组工人每小时共可生产口罩![]() 只,若
只,若![]() 两组工人每小时至少加工
两组工人每小时至少加工![]() 只口罩,那么
只口罩,那么![]() 组工人每人每小时至少加工多少只口罩?
组工人每人每小时至少加工多少只口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= ![]() 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(![]() ,n).连接OB,若S△AOB=1.
,n).连接OB,若S△AOB=1.
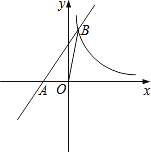
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组 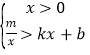 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
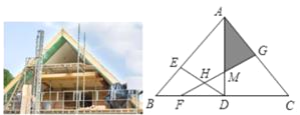
【题目】工人师傅在修茸一人字架屋顶BAC时需要加固,计划焊接三根钢条AD,DE,FG.在如图所示的△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E,F,G分别是AB,BD,AC上的点,连接DE,GF,交于点H,GF与AD交于点M,当H为FM的中点,BF∶CF=1∶5,AG:AE=5:7时,△AGM的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
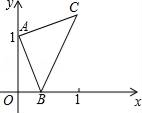
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.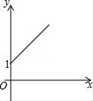 B.
B.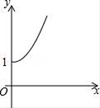
C.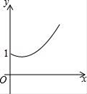 D.
D.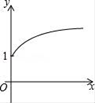
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现:如图①,点A为一动点,点B和点C为两个定点,且![]() ,
,![]() (
(![]() ).
).
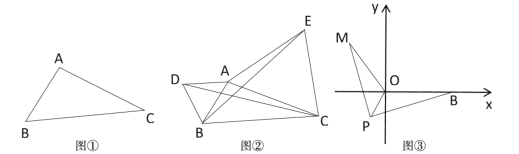
填空:当点![]() 位于_______时,线段
位于_______时,线段![]() 的长取得最小值,且最小值为_______(用含
的长取得最小值,且最小值为_______(用含![]() 的式子表示);
的式子表示);
(2)如图②应用:点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,如图2分别以
,如图2分别以![]() 、
、![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 、
、![]() .
.
①请找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最小值.
长的最小值.
(3)拓展:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段OB外一动点,且
为线段OB外一动点,且![]() ,
,![]() ,
,![]() ,请求出
,请求出![]() 的最小值并直接写出点
的最小值并直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
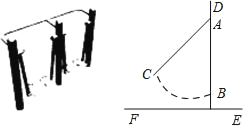
【题目】图1中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看图2,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°,求此时点C距离地面EF的高度.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com