
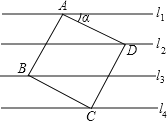
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】A
【解析】
过点D作DE⊥l1于点E并反向延长交l4于点F,根据同角的余角相等求出∠α=∠CDF,根据正方形的每条边都相等可得AD=DC,然后利用“AAS”证明△ADE和△DCF全等,根据全等三角形对应边相等可得DF=AE,再利用勾股定理列式求出AD的长度,然后根据锐角的余弦值等于邻边比斜边列式计算即可得解.
解:如图,过点D作DE⊥l1于点E并反向延长交l4于点F,
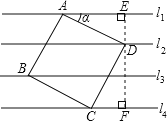
在正方形ABCD中,AD=DC,∠ADC=90°,
∵∠α+∠ADE=90°,∠ADE+∠CDF=180°-90°=90°,
∴∠α=∠CDF,
在△ADE和△DCF中,
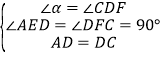
∴△ADE≌△DCF(AAS),
∴DF=AE,
∵相邻两条平行直线间的距离都是1,
∴DE=1,AE=2,
根据勾股定理得,AD=![]() =
=![]() =
=![]() ,
,
所以,cosα=![]() =
=![]() =
=![]() .
.
故选:A.


科目:初中数学 来源: 题型:
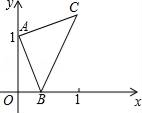
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.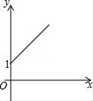 B.
B.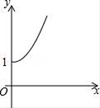
C.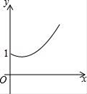 D.
D.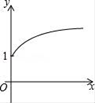
查看答案和解析>>
科目:初中数学 来源: 题型:
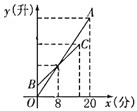
【题目】一个蓄水池有甲、乙两个注水管和一个排水管丙,三个水管均已关闭,已知乙注水管的注水速度为10升/分.先打开乙注水管4分钟,再打开甲注水管,甲、乙两个水管均注水20分钟.设甲注水管的工作时间为![]() (分),甲注水管的注水量
(分),甲注水管的注水量![]() (升)与时间
(升)与时间![]() (分)的函数图象为线段
(分)的函数图象为线段![]() ,乙注水管的注水量
,乙注水管的注水量![]() (升)与时间
(升)与时间![]() (分)的函数图象为线段
(分)的函数图象为线段![]() ,如图所示.
,如图所示.
(1)求甲注水管的总注水量;
(2)求线段![]() 所对应的函数关系式,并写出自变量的取值范围;
所对应的函数关系式,并写出自变量的取值范围;
(3)乙注水管打开的16分钟后,打开丙出水管.已知出水管丙的排水速度为20升/分,求丙出水管打开多长时间能将蓄水池的水排空.
查看答案和解析>>
科目:初中数学 来源: 题型:
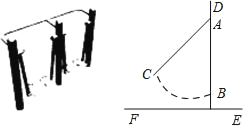
【题目】图1中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看图2,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°,求此时点C距离地面EF的高度.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
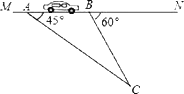
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
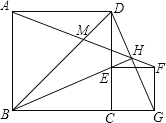
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为![]() ,则这块圆形纸片的直径为( )
,则这块圆形纸片的直径为( )
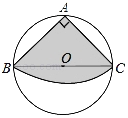
A. 12cm B. 20cm C. 24cm D. 28cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圆![]() 中,
中,![]() 、
、![]() 是圆
是圆![]() 的半径,点
的半径,点![]() 在劣弧
在劣弧![]() 上,
上,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
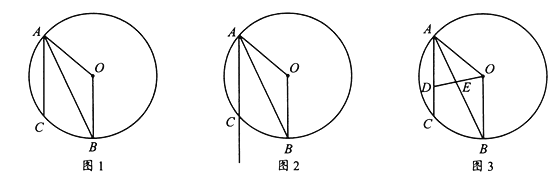
(1)如图1,试说明:![]() 平分
平分![]() ;
;
(2)如图2,点![]() 在弦
在弦![]() 的延长线上,连接
的延长线上,连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长;
的长;
(3)如图3,点![]() 在弦
在弦![]() 上,与点
上,与点![]() 不重合,连接
不重合,连接![]() 与弦
与弦![]() 交于点
交于点![]() ,设点
,设点![]() 与点
与点![]() 的距离为
的距离为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com