
某商场将进价为30元的台灯按40元出售,平均每月能售出600盏.调查表 明,这种台灯的售价每上涨1元,其销售量减少10盏.为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少元?这时应进台灯多少盏?
明,这种台灯的售价每上涨1元,其销售量减少10盏.为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少元?这时应进台灯多少盏?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
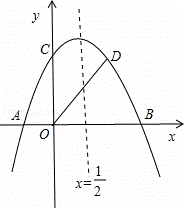
如图,抛物线 与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,对称轴为直线
与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,对称轴为直线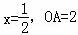 ,OD平分∠BOC交抛物线于点D(点D在第一象限).
,OD平分∠BOC交抛物线于点D(点D在第一象限).
(1)求抛物线的解析式和点D的坐标;
(2)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点M是抛物线上的动点,在x轴上是否存在点N,使A、D、M、N四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的M点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
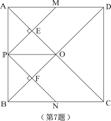
如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;
⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示的直角坐标系中,O为坐标原点,直线y=-x+m与x轴、y轴交于A、 B两点,且A的坐标为(4,0)。(1)求m的值。(2)若直线OP与线段AB交于点P,且AP:AB=1:4,求P的坐标。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com