
分析 (1)当k=1时,把y=x2-x-2配成顶点式即可对①解析判断;当k=2时,y=2x2-2,抛物线的对称轴为y轴,则可对②解析判断;根据二次函数图象上点的坐标特征对③解析判断;
(2)分类讨论:当k=0时,原函数为一次函数y=-2x-2,则图象一定与x轴有一个交点;当k≠0时,利用判别式的意义可判断二次函数图象与x轴有交点,所以无论k为何值时,函数图象与x轴总有交点;
(3)利用抛物线与x轴的交点问题,解方程kx2+(k-2)x-2=0可得A($\frac{2}{k}$,0),B(-1,0),顶点P的坐标为( $\frac{2-k}{2k}$,-$\frac{(k+2)^{2}}{4k}$),当k>0时,AB=$\frac{2}{k}+1$,如图1,作PE⊥x轴于E,根据等边三角形的性质得PE=$\frac{\sqrt{3}}{2}$AB,即 $\frac{(k+2)^{2}}{4k}$=$\frac{\sqrt{3}}{2}$×$(\frac{2}{k}+1)$,解得k1=-2(舍去),k2=2$\sqrt{3}$-2,所以k的值为2$\sqrt{3}$-2.
解答 (1)解:当k=1时,y=x2-x-2=(x-$\frac{1}{2}$)2-$\frac{9}{4}$,此时顶点坐标为($\frac{1}{2}$,-$\frac{9}{4}$),所以①错误;
当k=2时,y=2x2-2,则抛物线的对称轴为y轴,所以②正确;
当x=-1时,y=kx2+(k-2)x-2=k-k+2-2=0;当x=0时,y=kx2+(k-2)x-2=-2,所以无论k为何非零值,二次函数都经过(-1,0)和(0,-2),所以③正确;
故答案为:②③;
(2)证明:当k=0时,一次函数y=-2x-2与x轴有一个交点(-1,0);
当k≠0时,△=(k-2)2-4k•(-2)=(k+2)2≥0,此二次函数图象与x轴有交点,
所以无论k为何值时,函数图象与x轴总有交点;
(3)解:当y=0时,kx2+(k-2)x-2=0,解得x1=-1,x2=$\frac{2}{k}$,
设A($\frac{2}{k}$,0),B(-1,0),顶点P的坐标为($\frac{2-k}{2k}$,-$\frac{(k+2)^{2}}{4k}$),
AB=$\frac{2}{k}$+1,如图1,作PE⊥x轴于E.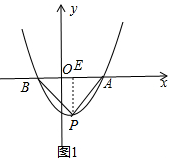
∵△ABP为等边三角形,
∴PE=$\frac{\sqrt{3}}{2}$AB,即 $\frac{(k+2)^{2}}{4k}$=$\frac{\sqrt{3}}{2}$×$(\frac{2}{k}+1)$,
解得k1=-2(舍去),k2=2$\sqrt{3}$-2,
∴k的值为2$\sqrt{3}$-2.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等边三角形的性质,列出关于k的方程是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
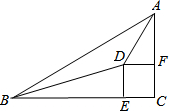 如图,△ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F;
如图,△ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
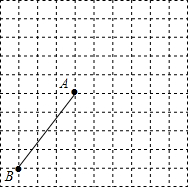 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
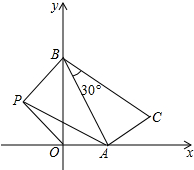 如图,一次函数y=-$\sqrt{3}x+\sqrt{3}$的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,使∠ABC=30°;
如图,一次函数y=-$\sqrt{3}x+\sqrt{3}$的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,使∠ABC=30°;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com