
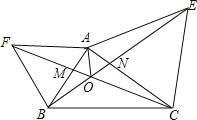
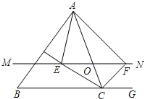
【题目】如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
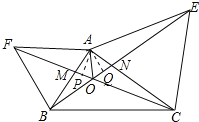
如图先证明△ABE≌△AFC,得到BE=CF,S△ABE=S△AFC,得到AP=AQ,利用角平分线的判定定理得AO平分∠EOF,再利用“8字型”证明∠CON=∠CAE=60°,由此可以解决问题.
解:∵AB=AF,AC=AE,∠FAB=∠EAC=60°,
∴∠FAB+∠BAC=∠EAC+∠BAC,
即∠FAC=∠BAE,
在△ABE与△AFC中,
 ,
,
∴△ABE≌△AFC(SAS),
∴BE=FC,故①正确,∠AEB=∠ACF,
∵∠EAN+∠ANE+∠AEB=180°,∠CON+∠CNO+∠ACF=180°,∠ANE=∠CNO,
∴∠CON=∠CAE=60°=∠MOB,
∴∠BOC=180°﹣∠CON=120°,故④正确,
连AO,过A分别作AP⊥CF与P,AM⊥BE于Q,如图,
∵△ABE≌△AFC,
∴S△ABE=S△AFC,
∴![]() CFAP=
CFAP=![]() BEAQ,而CF=BE,
BEAQ,而CF=BE,
∴AP=AQ,
∴OA平分∠FOE,所以③正确,
∵∠AMO=∠MOB+∠ABE=60°+∠ABE,∠ANO=∠CON+∠ACF=60°+∠ACF,
显然∠ABE与∠ACF不一定相等,
∴∠AMO与∠ANO不一定相等,故②错误,
综上所述正确的有:①③④.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的高,连接
的高,连接![]() 交
交![]() 于
于![]() .下列结论:①
.下列结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() 平分
平分![]() ;④当
;④当![]() 为
为![]() 时,
时,![]() ,其中不正确的结论的个数为( )
,其中不正确的结论的个数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
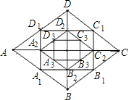
【题目】如图,以菱形![]() 各边的中点为顶点作四边形
各边的中点为顶点作四边形![]() ,再以
,再以![]() 各边的中点为顶点作四边形
各边的中点为顶点作四边形![]() ,…,如此下去,得到四边形
,…,如此下去,得到四边形![]() ,若
,若![]() 对角线长分别为
对角线长分别为![]() 和
和![]() ,请用含
,请用含![]() 、
、![]() 的代数式表示四边形
的代数式表示四边形![]() 的周长________.
的周长________.
查看答案和解析>>
科目:初中数学 来源: 题型:
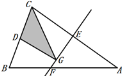
【题目】如图,等腰三角形ABC的底边BC长为4,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点G为线段EF上一动点,则△CDG周长的最小值为( )
A.7B.9C.11D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,点
中,点![]() 是边
是边![]() 上一个动点,过
上一个动点,过![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当点
当点![]() 在
在![]() 上运动到何处时,四边形
上运动到何处时,四边形![]() 为矩形?请说明理由;
为矩形?请说明理由;
![]() 当点
当点![]() 在
在![]() 上运动时,四边形
上运动时,四边形![]() 能为菱形吗?请说明理由.
能为菱形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
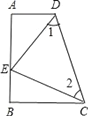
【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生下学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | m | b |
12<x≤15 | 4 | 0.08 |
15<x≤18 | 2 | n |
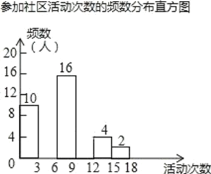
根据以上图表信息,解答下列问题:
(1)表中a=___,b=___;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1500名学生,请估计该校在下学期参加社区活动超过6次的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=-x2+bx+c经过A(0,-2),B(-1,1)两点,那么此抛物线经过
A. 第一、二、三、四象限 B. 第一、二、三象限
C. 第一、二、四象限 D. 第二、三、四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com