
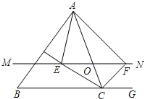
【题目】如图,![]() 中,点
中,点![]() 是边
是边![]() 上一个动点,过
上一个动点,过![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当点
当点![]() 在
在![]() 上运动到何处时,四边形
上运动到何处时,四边形![]() 为矩形?请说明理由;
为矩形?请说明理由;
![]() 当点
当点![]() 在
在![]() 上运动时,四边形
上运动时,四边形![]() 能为菱形吗?请说明理由.
能为菱形吗?请说明理由.
【答案】(1)见解析;(2)当点![]() 在边
在边![]() 上运动到
上运动到![]() 中点时,四边形
中点时,四边形![]() 是矩形,理由见解析;(3)不可能,理由见解析
是矩形,理由见解析;(3)不可能,理由见解析
【解析】
(1)由直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,易证得OE=OC,同理可证OC=OF,则可证得OE=OF=OC;
(2)根据平行四边形的判定以及矩形的判定得出即可.
(3)菱形的判定问题,若使菱形,则必有四条边相等,对角线互相垂直,进而分析求出即可.
![]() 证明:∵
证明:∵![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可证![]() ,
,
∴![]() ;
;![]() 解:当点
解:当点![]() 在边
在边![]() 上运动到
上运动到![]() 中点时,四边形
中点时,四边形![]() 是矩形.
是矩形.
理由是:当![]() 为
为![]() 的中点时,
的中点时,![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,

∴平行四边形![]() 是矩形.
是矩形.![]() 解:不可能.
解:不可能.
理由如下:如图,连接![]() ,
,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,
若四边形![]() 是菱形,则
是菱形,则![]() ,
,
但在![]() 中,不可能存在两个角为
中,不可能存在两个角为![]() ,所以不存在其为菱形.
,所以不存在其为菱形.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为P(2,9),与x轴交于点A,B,与y轴交于点C(0,5).
(Ⅰ)求二次函数的解析式及点A,B的坐标;
(Ⅱ)设点Q在第一象限的抛物线上,若其关于原点的对称点Q′也在抛物线上,求点Q的坐标;
(Ⅲ)若点M在抛物线上,点N在抛物线的对称轴上,使得以A,C,M,N为顶点的四边形是平行四边形,且AC为其一边,求点M,N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,点
,点![]() 为
为![]() 三条角平分线的交点,
三条角平分线的交点,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到三边
到三边![]() 、
、![]() 、
、![]() 的距离为( )
的距离为( )
A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
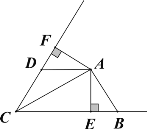
【题目】如图,AC平分∠BCD,AB=AD, AE⊥BC于E,AF⊥CD于F
(1)若∠ABE= 50° ,求∠CDA的度数.
(2)若AE=4,BE=2,CD=6,求四边形AECD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
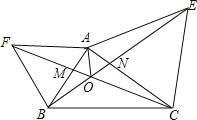
【题目】如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
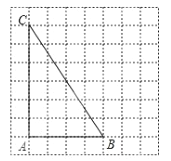
【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在![]() 上找一点P,使点P到
上找一点P,使点P到![]() 和
和![]() 的距离相等;
的距离相等;
②在射线![]() 上找一点Q,使
上找一点Q,使![]() .
.
(2)在(1)中连接![]() 与
与![]() ,试说明
,试说明![]() 是直角三角形.
是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2 200元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com