【题目】
中，
，点
为三条角平分线的交点，
于
，
于
，
于
，且
，
，
，则点到三边
、
、
的距离为（ ）
A. 2cm，2cm，2cm B. 3cm，3cm，3cm
C. 4cm，4cm，4cm D. 2cm，3cm，5cm
【答案】A
【解析】
由角平分线的性质可得OE=OF=OD，AE=AF，CE=CD，BD=BF，设OE=OF=OD=x，则CE=CD=x，BD=BF=8-x，AF=AE=6-x，所以6-x+8-x=10，由此即可解答．
如图，连接OB，
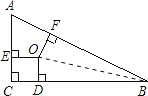
∵点O为△ABC的三条角平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB，点D、E、F分别是垂足，
∴OE=OF=OD，
又∵OB是公共边，
∴Rt△BOF≌Rt△BOD（HL），
∴BD=BF，
同理，AE=AF，CE=CD，
∵∠C=90°，OD⊥BC，OE⊥AC，OF⊥AB，OD=OE，
∴OECD是正方形，
设OE=OF=OD=x，则CE=CD=x，BD=BF=8-x，AF=AE=6-x，
∴BF+FA=AB=10，即6-x+8-x=10，
解得x=2．
则OE=OF=OD=2．
故选A．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，延长AB到点E,连接EC,使得∠BCE=∠BAC
(1)求证：EC是⊙O的切线；
（2）过点A作AD⊥EC的延长线于点D,若AD=5，DE=12，求⊙O的半径.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
边上有一点
（点不与点
、点
重合），过点作直线截
，使截得的三角形与相似，满足条件的直线共有（ ）
A. 2条 B. 3条 C. 4条 D. 5条
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是（﹣2，3），先把△ABC向右平移4个单位长度得到△A1B1C1，再作与△A1B1C1关于x轴对称的△A2B2C2 ．
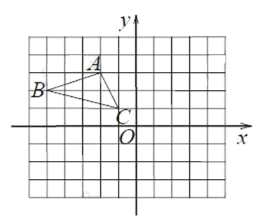
（1）在图中画出△A1B1C1和△A2B2C2 ；
（2）点A2的坐标为 ；
（3）求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与
轴交于点
，与
轴交于点
、
，点坐标为
．
求该抛物线的解析式；
抛物线的顶点为
，在轴上找一点
，使
最小，并求出点的坐标；
点
是线段
上的动点，过点作
，交
于点
，连接
．当
的面积最大时，求点的坐标；
若平行于轴的动直线
与该抛物线交于点
，与直线
交于点
，点
的坐标为
．问：是否存在这样的直线，使得
是等腰三角形？若存在，请求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，直线y＝﹣
x+
与y＝x相交于点A，与x轴交于点B.
(1)填空：A的坐标是_______，B的坐标是___________；
(2)直线y＝﹣x+上有点P(m，n)，且点P在第四象限，设△AOP的面积为S，请求出S与m的函数关系式；
(3)在直线OA上，是否存在一点D，使得△DOB是等腰三角形？如果存在，试求出所有符合条件的点D的坐标，如果不存在，请说明理由.
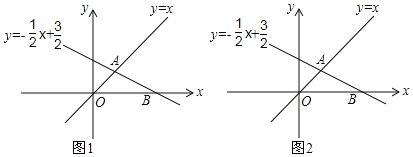
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的材料：把形如
的二次三项式（或其中一部分）配成完全平方的形式，叫做配方法．配方的基本形式是完全平方公式的逆运用，即
．
例如：
________
________
________．
以上是
的三种不同形式的配方（即“余项”分别是常数、一次项、二次项–见横线上的部分）．根据阅读材料解决以下问题：
仿照上面的例子，写出
三种不同形式的配方；
将
配方（至少写出两种形式）；
已知
，求
、
、
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．
（1）求证：△ABE≌△ACF；
（2）若∠BAE=30°，则∠ADC= °．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
