
【题目】如图,![]() 是
是![]() 的外角,
的外角,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() 、
、![]() 交于点
交于点![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)猜想:若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)见解析;(2)25°
【解析】
(1)首先根据角平分线的性质,得出∠ACE=∠DCE,又由![]() 得出∠ABC=∠DCE,然后根据同位角相等,两直线平行即可判定
得出∠ABC=∠DCE,然后根据同位角相等,两直线平行即可判定![]() ;
;
(2)首先由![]() 得出∠A=∠ACE,∠ABE=∠BEC,然后由角平分线的性质,得出∠ABE=∠DBE,进而得出∠BEC=∠DBE,最后由外角的性质,即可得解.
得出∠A=∠ACE,∠ABE=∠BEC,然后由角平分线的性质,得出∠ABE=∠DBE,进而得出∠BEC=∠DBE,最后由外角的性质,即可得解.
(1)∵![]() 平分
平分![]() ,
,
∴∠ACE=∠DCE
又∵![]()
∴∠ABC=∠DCE
∴![]() (同位角相等,两直线平行)
(同位角相等,两直线平行)
即可得证.
(2)由(1)中![]() ,得
,得
∠A=∠ACE,∠ABE=∠BEC
∵![]() 平分
平分![]() ,
,
∴∠ABE=∠DBE
∴∠BEC=∠DBE
又∵∠DCE=∠ACE=∠BEC+∠DBE=50°
∴ ∠E=25°
故答案为25°.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则tan∠AEF的值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
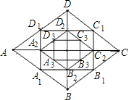
【题目】如图,以菱形![]() 各边的中点为顶点作四边形
各边的中点为顶点作四边形![]() ,再以
,再以![]() 各边的中点为顶点作四边形
各边的中点为顶点作四边形![]() ,…,如此下去,得到四边形
,…,如此下去,得到四边形![]() ,若
,若![]() 对角线长分别为
对角线长分别为![]() 和
和![]() ,请用含
,请用含![]() 、
、![]() 的代数式表示四边形
的代数式表示四边形![]() 的周长________.
的周长________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,点
,点![]() 为
为![]() 三条角平分线的交点,
三条角平分线的交点,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到三边
到三边![]() 、
、![]() 、
、![]() 的距离为( )
的距离为( )
A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
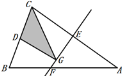
【题目】如图,等腰三角形ABC的底边BC长为4,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点G为线段EF上一动点,则△CDG周长的最小值为( )
A.7B.9C.11D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
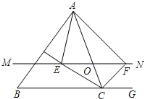
【题目】如图,![]() 中,点
中,点![]() 是边
是边![]() 上一个动点,过
上一个动点,过![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当点
当点![]() 在
在![]() 上运动到何处时,四边形
上运动到何处时,四边形![]() 为矩形?请说明理由;
为矩形?请说明理由;
![]() 当点
当点![]() 在
在![]() 上运动时,四边形
上运动时,四边形![]() 能为菱形吗?请说明理由.
能为菱形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生下学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | m | b |
12<x≤15 | 4 | 0.08 |
15<x≤18 | 2 | n |
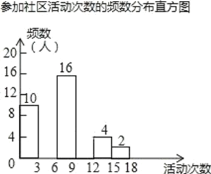
根据以上图表信息,解答下列问题:
(1)表中a=___,b=___;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1500名学生,请估计该校在下学期参加社区活动超过6次的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com