
【题目】如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则tan∠AEF的值是_____.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
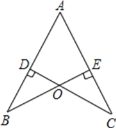
【题目】如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)问题探究:线段OB,OC有何数量关系,并说明理由;
(2)问题拓展:分别连接OA,BC,试判断直线OA,BC的位置关系,并说明理由;
(3)问题延伸:将题目条件中的“CD⊥AB于D,BE⊥AC于E”换成“D、E分别为AB,AC边上的中点”,(1)(2)中的结论还成立吗?请直接写出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,BE=EC,将正方形ABCD的边CD沿DE折叠到DF,连接EF、FC、FB,若△DFC的面积为16,则△BEF的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列五个结论:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,则
;③ON⊥OM;④若AB=2,则![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正确结论是_________.(只填番号)
.其中正确结论是_________.(只填番号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为P(2,9),与x轴交于点A,B,与y轴交于点C(0,5).
(Ⅰ)求二次函数的解析式及点A,B的坐标;
(Ⅱ)设点Q在第一象限的抛物线上,若其关于原点的对称点Q′也在抛物线上,求点Q的坐标;
(Ⅲ)若点M在抛物线上,点N在抛物线的对称轴上,使得以A,C,M,N为顶点的四边形是平行四边形,且AC为其一边,求点M,N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com