
【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
【答案】(I)C(3,0),B(1,4)A(6,9);(II)![]() <t<5;(III)
<t<5;(III)![]()
【解析】分析:(Ⅰ)将抛物线的一般式配方为顶点式即可求出点C的坐标,联立抛物线与直线的解析式即可求出A、B的坐标.
(Ⅱ)由题意可知:新抛物线的顶点坐标为(3﹣t,1),然后求出直线AC的解析式后,将点E的坐标分别代入直线AC与AD的解析式中即可求出t的值,从而可知新抛物线的顶点E在△DAC内,求t的取值范围.
(Ⅲ)直线AB与y轴交于点F,连接CF,过点P作PM⊥AB于点M,PN⊥x轴于点N,交DB于点G,由直线y=x+3与x轴交于点D,与y轴交于点F,得D(﹣3,0),F(0,3),易得CF⊥AB,△PAB的面积是△ABC面积的2倍,所以![]() ABPM=
ABPM=![]() ABCF,PM=2CF=6
ABCF,PM=2CF=6![]() ,从而可求出PG=12,利用点G在直线y=x+3上,P(m,n),所以G(m,m+3),所以PG=n﹣(m+3),所以n=m+15,由于P(m,n)在抛物线y=x2﹣6x+9上,联立方程从而可求出m、n的值.
,从而可求出PG=12,利用点G在直线y=x+3上,P(m,n),所以G(m,m+3),所以PG=n﹣(m+3),所以n=m+15,由于P(m,n)在抛物线y=x2﹣6x+9上,联立方程从而可求出m、n的值.
详解:(I)∵y=x2﹣6x+9=(x﹣3)2,∴顶点坐标为(3,0).
联立![]() ,
,
解得:![]() 或
或![]() ;
;
(II)由题意可知:新抛物线的顶点坐标为(3﹣t,1),设直线AC的解析式为y=kx+b
将A(1,4),C(3,0)代入y=kx+b中,∴![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为y=﹣2x+6.
当点E在直线AC上时,﹣2(3﹣t)+6=1,解得:t=![]() .
.
当点E在直线AD上时span>,(3﹣t)+3=1,解得:t=5,
∴当点E在△DAC内时,![]() <t<5;
<t<5;
(III)如图,直线AB与y轴交于点F,连接CF,过点P作PM⊥AB于点M,PN⊥x轴于点N,交DB于点G.
由直线y=x+3与x轴交于点D,与y轴交于点F,
得D(﹣3,0),F(0,3),∴OD=OF=3.
∵∠FOD=90°,∴∠OFD=∠ODF=45°.
∵OC=OF=3,∠FOC=90°,
∴CF=![]() =3
=3![]() ,∠OFC=∠OCF=45°,
,∠OFC=∠OCF=45°,
∴∠DFC=∠DFO+∠OFC=45°+45°=90°,∴CF⊥AB.
∵△PAB的面积是△ABC面积的2倍,∴![]() ABPM=
ABPM=![]() ABCF,
ABCF,
∴PM=2CF=6![]() .
.
∵PN⊥x轴,∠FDO=45°,∴∠DGN=45°,∴∠PGM=45°.
在Rt△PGM中,sin∠PGM=![]() , ∴PG=
, ∴PG=![]() =
=![]() =12.
=12.
∵点G在直线y=x+3上,P(m,n), ∴G(m,m+3).
∵﹣3<m<1,∴点P在点G的上方,∴PG=n﹣(m+3),∴n=m+15.
∵P(m,n)在抛物线y=x2﹣6x+9上,
∴m2﹣6m+9=n,∴m2﹣6m+9=m+15,解得:m=![]() .
.
∵﹣3<m<1,∴m=![]() 不合题意,舍去,∴m=
不合题意,舍去,∴m=![]() ,∴n=m+15=
,∴n=m+15=![]() .
.



 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
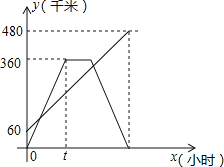
【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
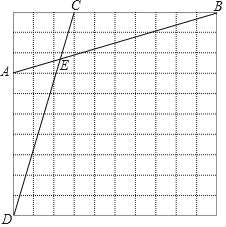
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D均在格点上,AB与CD相交于点E.
(Ⅰ)AB的长等于 ;
(Ⅱ)点F是线段DE的中点,在线段BF上有一点P,满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险救灾中,某地粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到没有受洪水威胁的A,B两仓库,已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为60吨,B库的容量为120吨,从甲、乙两库到A、B两库的路程和运费如表(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
若从甲库运往A库粮食x吨,
(Ⅰ)填空(用含x的代数式表示):
①从甲库运往B库粮食 吨;
②从乙库运往A库粮食 吨;
③从乙库运往B库粮食 吨;
(Ⅱ)写出将甲、乙两库粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式,并求出当从甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从某点![]() 出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
(1)小虫离开出发点![]() 最远是多少厘米?
最远是多少厘米?
(2)小虫最后是否回到原点![]() ?
?
(3)在爬行过程中看,如果每爬行1cm奖励2粒芝麻,则小虫共可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
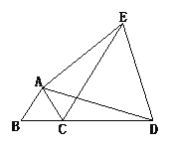
【题目】已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,用你学过的知识探索AC、CD、CE三条线段的长度有何关系?试写出探求过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com