
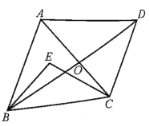
【题目】如图所示,在四边形ABCD中,对角线AC,BD相交于点O,点E在![]() 的内部,连接EB,EC,说明:
的内部,连接EB,EC,说明:
(1)![]() ;
;
(2)![]() ;
;
(3)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)在△ABO和△DCO中,根据两边之和大于第三边,列出不等式,相加即可得到结论;
(2)延长BE交AC于点F.在△ABF和△CEF中根据两边之和大于第三边,列出不等式,相加即可得到结论;
(3)由(2)可知,EB+EC<13.在△EBC中,根据两边之和大于第三边,即可得到结论.
(1)在△ABO中,AB<AO+BO,①
在△DCO中,CD<CO+DO,②
①+②得:AB+CD<AO+BO+CO+DO,
即AB+CD<AC+BD.
(2)如图所示,

延长BE交AC于点F.
∵在△ABF中,AB+AF>BF=BE+FE,①
在△CEF中,FE+FC>EC,②
由①+②得:
AB+(AF+FC)+FE>BE+EC+FE
即AB+AC>EB+EC.
(3)由(2)可知,EB+EC<13,
在△EBC中,EB+EC>BC,且BC=11,
∴11<EB+EC<13.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的两个互相重合的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度α(0°<α<90°),若两正方形重叠部分的面积为![]() ,则这个旋转角度为_____度.
,则这个旋转角度为_____度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有下列说法:①若
有下列说法:①若![]() ,则
,则![]() ;②若方程两根为-1和2,则
;②若方程两根为-1和2,则![]() ;③若方程
;③若方程![]() 有两个不相等的实根,则方程
有两个不相等的实根,则方程![]() 必有两个不相等的实根;④若
必有两个不相等的实根;④若![]() ,则方程有两个不相等的实根,其中结论正确的是有( )个。
,则方程有两个不相等的实根,其中结论正确的是有( )个。
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x,y轴交于点D,C,这两条直线交于点E.
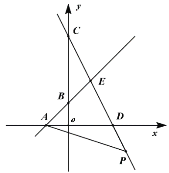
(1)求E点坐标;
(2)若P为直线CD上一点,当△ADP的面积为9时,求P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是直角,
是直角,![]() 平分
平分![]() .
.
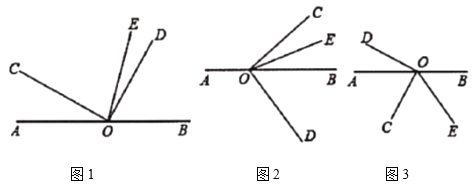
(1)如图1,若![]() ,则
,则![]() 的度数为___________;
的度数为___________;
(2)如图1,若![]() ,则
,则![]() 的度数为__________(用含有
的度数为__________(用含有![]() 的式子表示);
的式子表示);
(3)将图1中的![]() 绕顶点
绕顶点![]() 顺时针旋转至图2的位置,试探究
顺时针旋转至图2的位置,试探究![]() 和
和![]() 度数之间的关系,写出你的结论,并说明理由.
度数之间的关系,写出你的结论,并说明理由.
(4)将图1中的![]() 绕顶点
绕顶点![]() 逆时针旋转至图3的位置,其它条件不变,若
逆时针旋转至图3的位置,其它条件不变,若![]() ,则
,则![]() 的度数为____________.(用含有
的度数为____________.(用含有![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:
(1)在甲店购买需付款 元,在乙店购买需付款 元;
(2)若x=30,通过计算说明此时到哪家商店购买较为合算?
(3)当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班开展勤俭节约的活动,对每个同学的一天的消费情况进行调查,得到统计图如图所示:
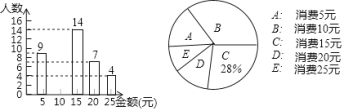
(1)求该班的总人数;
(2)将条形图补充完整,并写出消费金额的中位数;
(3)该班这一天平均每人消费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为边BC上一点,E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,连结BF.
(1)求证:四边形ADBF是平行四边形;
(2)当D为边BC的中点,且BC=2AC时,求证:四边形ACDF为正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com