
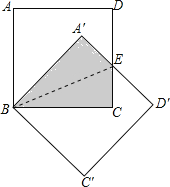
【题目】如图,将边长为2cm的两个互相重合的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度α(0°<α<90°),若两正方形重叠部分的面积为![]() ,则这个旋转角度为_____度.
,则这个旋转角度为_____度.

【答案】30°
【解析】分析:设A′D′与CD的交点为E,连接BE;由于A′B=BC,易证得△A′BE≌△CBE,因此两者的面积相等,即可根据△CBE的面积求得CE的值,从而通过解直角三角形求出∠CBE、∠CBA′的度数,进而可求得旋转角的度数.
详解:设A′D′与CD的交点为E,连接BE.
∵A′B=BC,BE=BE,
∴Rt△A′BE≌Rt△CBE.(HL)
∴∠A′BE=∠EBC,且S△BA′E=S△BCE=![]() .
.
在Rt△BCE中,BC=2,则:
S△BCE=![]() ×2×CE=
×2×CE=![]() ,
,
∴CE=![]() .
.
∴tan∠EBC=![]() ,即∠EBC=30°.
,即∠EBC=30°.
∴∠A′BC=2∠EBC=60°,∠ABA′=90°-∠A′BC=30°.
故旋转的角度为30°.


科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一四柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示,根据图象提供的信息,解答下列问题:
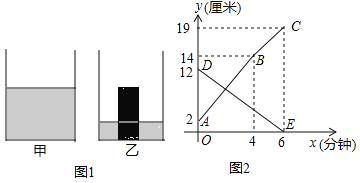
(1)图2中折线ABC表示 槽中水的深度与注水时间关系,线段DE表示 槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点B的纵坐标表示的实际意义是 .
(2)注水多长时间时,甲、乙.两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),则乙槽中铁块的体积为 立方厘米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:![]() 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有![]() .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)![]() ;(2)
;(2)![]() ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
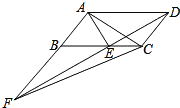
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
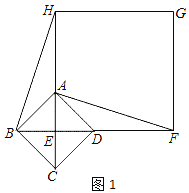
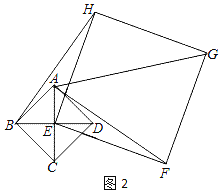
【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,直接写出BH和AF的数量关系;
(2)将正方形EFGH绕点E顺时针方向旋转.
①如图2,判断BH和AF的数量关系,并说明理由;
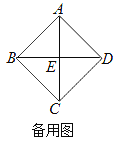
②如果四边形ABDH是平行四边形,请在备用图中补全图形;如果四方形ABCD的边长为![]() ,求正方形EFGH的边长.
,求正方形EFGH的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
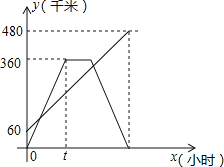
【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com