
【题目】某班开展勤俭节约的活动,对每个同学的一天的消费情况进行调查,得到统计图如图所示:
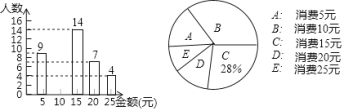
(1)求该班的总人数;
(2)将条形图补充完整,并写出消费金额的中位数;
(3)该班这一天平均每人消费多少元?
【答案】(1)50;(2)图详见解析,12.5;(3)该班这一天平均每人消费13.1元.
【解析】
(1)根据C类有14人,占28%,即可求得该班的总人数;(2)根据(1)中的答案可以求得消费10元的人数,从而可以将条形统计图补充完整,进而求得消费金额的中位数;(3)根据加权平均数的计算方法可以求得该班这一天平均每人消费的金额.
(1)由题意可得,
该班的总人数为:14÷28%=50,
即该班的总人数是50;
(2)消费10元的有:50-9-14-7-4=16(人),
补充完整的统计图如图所示,
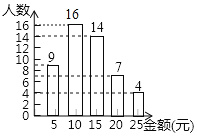
消费金额的中位数是:![]() =12.5;
=12.5;
(3)由题意可得,
该班这一天平均每人消费:![]() =13.1(元),
=13.1(元),
即该班这一天平均每人消费13.1元.


科目:初中数学 来源: 题型:
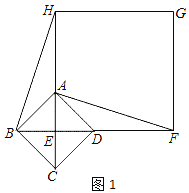
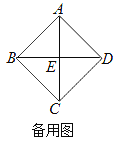
【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,直接写出BH和AF的数量关系;
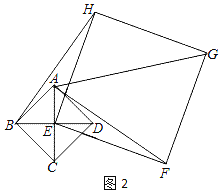
(2)将正方形EFGH绕点E顺时针方向旋转.
①如图2,判断BH和AF的数量关系,并说明理由;
②如果四边形ABDH是平行四边形,请在备用图中补全图形;如果四方形ABCD的边长为![]() ,求正方形EFGH的边长.
,求正方形EFGH的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
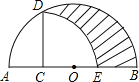
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店举行促销活动,具体办法如下:购买A品牌计算器按原价的九折销售,购买B品牌计算器超出10个以上超出的部分按原价的八折销售,①设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
②小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过10个,问购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
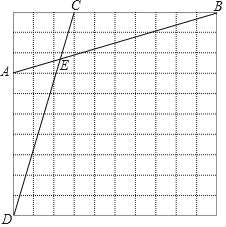
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D均在格点上,AB与CD相交于点E.
(Ⅰ)AB的长等于 ;
(Ⅱ)点F是线段DE的中点,在线段BF上有一点P,满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险救灾中,某地粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到没有受洪水威胁的A,B两仓库,已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为60吨,B库的容量为120吨,从甲、乙两库到A、B两库的路程和运费如表(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
若从甲库运往A库粮食x吨,
(Ⅰ)填空(用含x的代数式表示):
①从甲库运往B库粮食 吨;
②从乙库运往A库粮食 吨;
③从乙库运往B库粮食 吨;
(Ⅱ)写出将甲、乙两库粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式,并求出当从甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com