
【题目】小虫从某点![]() 出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
(1)小虫离开出发点![]() 最远是多少厘米?
最远是多少厘米?
(2)小虫最后是否回到原点![]() ?
?
(3)在爬行过程中看,如果每爬行1cm奖励2粒芝麻,则小虫共可得到多少粒芝麻?
【答案】(1)12cm;(2)小虫最后回到原点![]() ;(3)小虫可得到108粒芝麻.
;(3)小虫可得到108粒芝麻.
【解析】
(1)通过计算小虫每次爬完之后离原点的距离即可得出答案;
(2)利用有理数的加法进行计算然后看最后的结果是否为0,若为0,则回到原点,反之则没有;
(3)将每个数的绝对值相加,然后再乘2即可得出答案.
(1)根据题意可知,
小虫第一次爬完之后离原点的距离为5cm
小虫第二次爬完之后离原点的距离为![]()
小虫第三次爬完之后离原点的距离为![]()
小虫第四次爬完之后离原点的距离为![]()
小虫第五次爬完之后离原点的距离为![]()
小虫第六次爬完之后离原点的距离为![]()
小虫第七次爬完之后离原点的距离为![]()
∴小虫离开出发点![]() 最远是12cm.
最远是12cm.
(2)∵![]()
∴小虫最后回到原点![]() .
.
(3)![]() ,
,
![]() (粒)
(粒)
∴小虫可得到108粒芝麻.


科目:初中数学 来源: 题型:
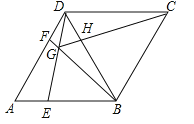
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB;②S四边形BCDG=![]() ;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
其中正确的结论个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:
(1)在甲店购买需付款 元,在乙店购买需付款 元;
(2)若x=30,通过计算说明此时到哪家商店购买较为合算?
(3)当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两座建筑物的水平距离BC为40m,从D点测得A点的仰角为30°,B点的俯角为10°,求建筑物AB的高度(结果保留小数点后一位).
参考数据sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,![]() 取1.732.
取1.732.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形 A BCD 中,对角线 A C、BD 相交于点 O,DE 平分∠A DO 交 AC 于点 E ,把 ![]() A DE 沿AD 翻折,得到
A DE 沿AD 翻折,得到![]() A DE’,点 F 是 DE 的中点,连接 A F、BF、E’F,若 AE=
A DE’,点 F 是 DE 的中点,连接 A F、BF、E’F,若 AE=![]() .
.
下列结论 :①AD 垂直平分 EE’,② tan∠ADE =![]() -1,
-1,
③ C![]() A DE - C
A DE - C![]() ODE =2
ODE =2![]() -1, ④ S四边形AEFE=
-1, ④ S四边形AEFE= ![]()
其中结论正确的个数是 ( ) .

A. 4 个 B. 3 个 C. 2 个 D. 1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
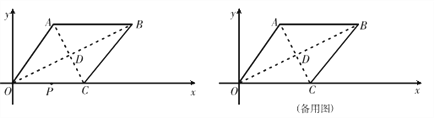
【题目】如图,在菱形 OA BC 中,已知点 B(8,4),C(5,0),
点 D 为 OB、AC 交点,点 P 从原点出发向 x 轴正方向运动;
(1) 在点 P 运动过程中,若∠OBP=900,求出点 P 坐标;
(2) 在点 P 运动过程中,若∠PDC+∠BCP=900,求出点 P 坐标;
(3) 点 P 在(2)的位置时停止运动,点 M 从点 P 出发沿 x 轴正方向运动,连结 BM,若点 P 关于BM 的对称点 P’到 AB 所在直线的距离为 2,求此时点 M 的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com