
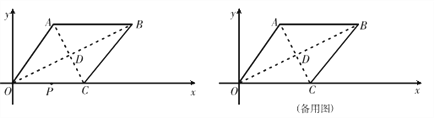
【题目】如图,在菱形 OA BC 中,已知点 B(8,4),C(5,0),
点 D 为 OB、AC 交点,点 P 从原点出发向 x 轴正方向运动;
(1) 在点 P 运动过程中,若∠OBP=900,求出点 P 坐标;
(2) 在点 P 运动过程中,若∠PDC+∠BCP=900,求出点 P 坐标;
(3) 点 P 在(2)的位置时停止运动,点 M 从点 P 出发沿 x 轴正方向运动,连结 BM,若点 P 关于BM 的对称点 P’到 AB 所在直线的距离为 2,求此时点 M 的坐标.
【答案】(1)(10,0)(2)(8,0)(3)点M的坐标为(8+![]() ,0)或(8+4
,0)或(8+4![]() ,0)
,0)
【解析】分析:(1)根据菱形的性质有OD=BD,![]() 根据∠OBP=90
根据∠OBP=90![]() ,得到CD∥BP,根据中位线的性质求解即可.
,得到CD∥BP,根据中位线的性质求解即可.
![]() 根据
根据![]() 得到
得到![]() ,求出
,求出![]() ,得到点P在以OB为直径的⊙D上,即可求解.
,得到点P在以OB为直径的⊙D上,即可求解.
![]() 过点P′作P′N⊥AB交直线AB于点N,交
过点P′作P′N⊥AB交直线AB于点N,交![]() 轴于点K,记BM与PP′交点为L,分点P′在直线AB下方时和点P′在直线AB上方时两种情况进行讨论即可.
轴于点K,记BM与PP′交点为L,分点P′在直线AB下方时和点P′在直线AB上方时两种情况进行讨论即可.
详解:(1)在菱形OABC中,有OD=BD,![]()
∵∠OBP=90![]() ,∴CD∥BP
,∴CD∥BP
∵OD=BD,∴OC=PC
∵C(5,0),
∴P![]()
(2)∵![]()
∴![]() ,
,
∵OC=BC,∴![]() ,
,
∵![]()
![]() ,
,
∴![]()
∴![]() ,
,
∵D为OB中点,
∴点P在以OB为直径的⊙D上,
∴![]()
故点P(8,0).

(3)过点P′作P′N⊥AB交直线AB于点N,交![]() 轴于点K,记BM与PP′交点为L
轴于点K,记BM与PP′交点为L
①如图,当点P′在直线AB下方时,
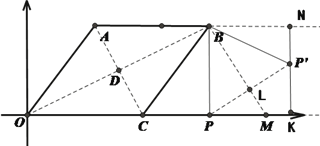
∵点P与点P′关于BM对称
∴![]()
∵![]() ,
,
∴Rt△BNP′≌Rt△PKP′,
∴ ![]()
即![]() 为等边三角形,
为等边三角形,
在Rt△PLM中,∵![]() ,∴PM2=22+(
,∴PM2=22+(![]() PM)2
PM)2
解得PM=![]() ,∴OM=8+
,∴OM=8+![]() ,
,
∴M1(8+![]() ,0),
,0),
②如图,当点P′在直线AB上方时
∵点P与点P′关于BM对称
∴![]()
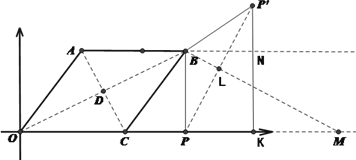
在![]() 中,
中,
∵![]() ′,∴
′,∴![]() ,
,
∴![]()
∵![]()
∵![]()
∵![]()
在Rt△BPM中,
∵BP=4,∴PM=![]() BP=4
BP=4![]()
∴OM=8+4![]() ,
,
∴M2(8+4![]() ,0)
,0)
故点M的坐标为(8+![]() ,0)或(8+4
,0)或(8+4![]() ,0)
,0)


科目:初中数学 来源: 题型:
【题目】列方程解应用题:
快放寒假了,小宇来到书店准备购买一些课外读物在假期里阅读.在选完书结账时,收银员告诉小宇,如果花20元办理一张会员卡,用会员卡结账买书,可以享受8折优惠.小宇心算了一下,觉得这样可以节省13元,很合算,于是采纳了收银员的意见.请根据以上信息解答下列问题:
(1)你认为小宇购买 元以上的书,办卡就合算了;
(2)小宇购买这些书的原价是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
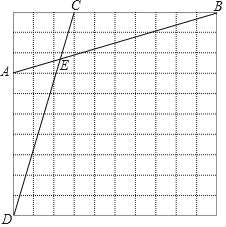
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D均在格点上,AB与CD相交于点E.
(Ⅰ)AB的长等于 ;
(Ⅱ)点F是线段DE的中点,在线段BF上有一点P,满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从某点![]() 出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
(1)小虫离开出发点![]() 最远是多少厘米?
最远是多少厘米?
(2)小虫最后是否回到原点![]() ?
?
(3)在爬行过程中看,如果每爬行1cm奖励2粒芝麻,则小虫共可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E分别在AC,AB上,且AD=AE,点O是BD和CE的交点,则:①△ABD≌△ACE;②△BOE≌△COD;③点O在∠BAC的平分线上,以上结论( )
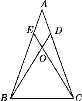
A.都正确B.都不正确
C.只有一个正确D.只有一个不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,用你学过的知识探索AC、CD、CE三条线段的长度有何关系?试写出探求过程.
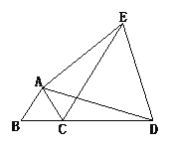
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图![]() ,
,![]() 分别为数轴上的两点,点
分别为数轴上的两点,点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数为80.
对应的数为80.

(1)请直接写出![]() 的中点
的中点![]() 对应的数.
对应的数.
(2)现在有一只电子蚂蚁![]() 从
从![]() 点出发,以2个单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发,以2个单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以3个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
点出发,以3个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇.请解答下面问题:
点相遇.请解答下面问题:
①试求出点![]() 在数轴上所对应的数;
在数轴上所对应的数;
②何时两只电子蚂蚁在数轴上相距15个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com