
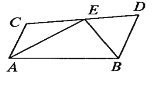
【题目】如图,![]() 分别平分
分别平分![]() 经过点
经过点![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
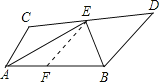
首先在AB上截取AF=AC,连接EF,证明△CAE≌△FAE,可证出∠CEA=∠FEA,可得到∠FEB=∠DEB,再证明△DEB≌△FEB,可得到BD=BF,即可证出AB=AC+BD.
在![]() 上取
上取![]() ,连接EF,
,连接EF,
在△CAE和△FAE中
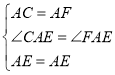
∴△CAE≌△FAE,
则∠CEA=∠FEA,
∵AC//BD,
∴∠CAB+∠DBA=180°,
∵AE,BE分别平分∠CAB,∠DBA,
∴∠FAE=![]() ∠CAB,∠FBE=
∠CAB,∠FBE=![]() ∠DAB
∠DAB
∴∠FAE+∠FBE=90°,∠AEB=180°-(∠FAE+∠FBE )=90°,
∴∠CEA+∠BED=∠FEA+∠FEB=90°,
∴∠FEB=∠DEB,
∵BE平分∠DBA,
∴∠DBE=∠FBE,
在△DEB和△FEB中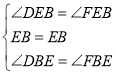
∴△DEB≌△FEB(ASA),
∴BD=BF,又∵AF=AC,
∴AB=AF+FB=AC+BD.
故选:B


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
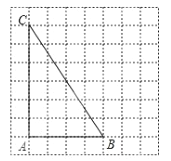
【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在![]() 上找一点P,使点P到
上找一点P,使点P到![]() 和
和![]() 的距离相等;
的距离相等;
②在射线![]() 上找一点Q,使
上找一点Q,使![]() .
.
(2)在(1)中连接![]() 与
与![]() ,试说明
,试说明![]() 是直角三角形.
是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·孝感)学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是 ( )
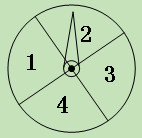
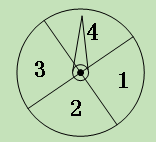
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历. 我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减,例如:![]() ,
,![]() ,不难发现,结果都是7.
,不难发现,结果都是7.
(1)请你再选择两个类似的部分试一试,看看是否符合这个规律;
(2)请你利用整式的运算对以上的规律加以证明.
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:
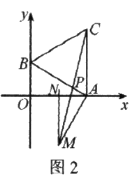
【题目】如图1,直角坐标系中,点![]() 分别在
分别在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() .以
.以![]() 为边在第一象限作等边
为边在第一象限作等边![]() 垂直平分
垂直平分![]() .
.
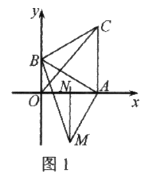
(1)求![]() 的长.
的长.
(2)求证:![]() .
.
(3)如图2,连接![]() 交
交![]() 于点
于点![]() .点
.点![]() 是否为MC的中点?请说明理由.
是否为MC的中点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2 200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,![]() 的顶点均在格点上,若
的顶点均在格点上,若![]() 点的坐标为
点的坐标为![]() 按要求回答案下列问题:
按要求回答案下列问题:
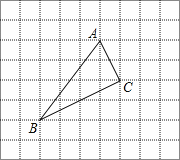
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,直接写出点![]() 和点
和点![]() 的坐标:
的坐标:![]() _______,
_______,![]() ________;
________;
(3)请画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ;
;
(4)在(3)的条件下,若![]() 是
是![]() 内部任意一点,请直接写出这点在
内部任意一点,请直接写出这点在![]() 内部的对应点
内部的对应点![]() 的坐标__________.
的坐标__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点D,E分别为边AB,AC上的点,且有AE=DB,连接DE,DC.
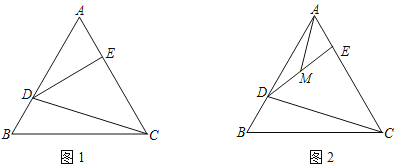
(1)如图1,若AB=6,∠DEC=90°,求△DEC的面积.
(2)M为DE中点,当D,E分别为AB、AC的中点时,判定CD,AM的数量关系并说明理由.
(3)如图2,M为DE中点,当D,E分别为AB,AC上的动点时,判定CD,AM的数量关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com