
����Ŀ����ͼ������������y1=k1x�뷴��������y2= ![]() �ཻ��A��B�㣮��֪��A������ΪA��4��n����BD��x���ڵ�D����S��BDO=4������A��һ�κ���y3=k3x+b�뷴����������ͼ������һ��C����x�ύ�ڵ�E��5��0����
�ཻ��A��B�㣮��֪��A������ΪA��4��n����BD��x���ڵ�D����S��BDO=4������A��һ�κ���y3=k3x+b�뷴����������ͼ������һ��C����x�ύ�ڵ�E��5��0���� 
��1��������������y1������������y2��һ�κ���y3�Ľ���ʽ��
��2�����ͼ�������k3x+b�� ![]() ��k1xʱx��ȡֵ��Χ��
��k1xʱx��ȡֵ��Χ��
���𰸡�
��1���⣺��S��BDO=4��
��k2=2��4=8��
�෴������������ʽ��y2= ![]() ��
��
�ߵ�A��4��n���ڷ���������ͼ���ϣ�
��4n=8��
n=2��
��A�������ǣ�4��2����
��A�㣨4��2��������������y1=k1xͼ���ϣ�
��2=k14��
k1= ![]() ��
��
����������������ʽ�ǣ�y1= ![]() x��
x��
��һ�κ���y3=k3x+b����A��4��2����E��5��0����
�� ![]() ��
��
��ã� ![]() ��
��
��һ�κ�������ʽΪ��y3=��2x+10
��2���⣺����y3=��2x+10��y2= ![]() ��
��
��ȥy�ã���2x+10= ![]() �����x1=1��x2=4��
�����x1=1��x2=4��
��һ����C�������ǣ�1��8����
��A��4��2���͵�B����ԭ�����ĶԳƣ�
��B����4����2����
���ɹ۲�ɵ�x��ȡֵ��Χ�ǣ�x����4����1��x��4
����������1�����ȸ��ݡ�BOD����������������������ʽ�������÷���������ͼ���ϵĵ���������A�����꣬������������������A�㣻�����ô���ϵ���������������������ʽ��һ�κ���y3=k3x+b����A��4��2����E��5��0�����ٴ����ô���ϵ�������һ�κ�������ʽ����2����C��һ�κ���y3=��2x+10�뷴������������ʽy2= ![]() �Ľ��㣬�÷��̩�2x+10=
�Ľ��㣬�÷��̩�2x+10= ![]() �����C�����꣬�����B�����꣬�����ͼ����Կ����𰸣�
�����C�����꣬�����B�����꣬�����ͼ����Կ����𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪4x2��mx+25����ȫƽ��ʽ������m��ֵΪ��������
A.10B.��10C.��20D.��20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
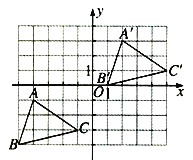
����Ŀ����ͼ��ʾ��������A��B��C����������ABC����ƽ�Ƶõ��ģ�A��-4��-1����B��-5��-4����������ABC������һ��P��x1��y1��ƽ�ƺ�Ķ�Ӧ��ΪP����x1+6��y1+4��.
��1����д��������ABCƽ�ƵĹ��̣�
��2���ֱ�д����A����B����C�������ꣻ
��3����������A��B��C�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC=90�㣬AC=2AB����D��AC���е㣮��һ�����Ϊ45���ֱ�����ǰ���ͼ���ã�ʹ���ǰ�б�ߵ������˵�ֱ���A��D�غϣ�����BE��EC���Բ����߶�BE��EC��������λ�ù�ϵ����֤����IJ��룮 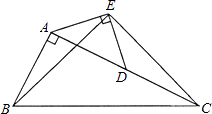
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в�����Ϊ�ж��ı���ABCDΪƽ���ı��ε��������ǣ� ��
A. AB��CD��AD��BC B. AB![]() CD
CD
C. AB��CD��AD��BC D. AB��CD��AD��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������ABCD�У�AD��BC����B��90����AD��24 �M��BC��26�M������P�ӵ�A��ʼ��AD����ÿ��1�M���ٶ���D���˶�������Q�ӵ�C��ʼ��CB����ÿ��3�M���ٶ���B�˶���P��Q�ֱ��A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt s��
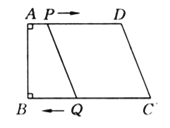
��1��tΪ��ֵʱ���ı���PQCDΪƽ���ı���?
��2��tΪ��ֵʱ���ı���PQCDΪ��������?
��3��tΪ��ֵʱ���ı���ABQPΪ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��D��BC������һ�㣬��D�ֱ���AB��AC�����ߣ�����ֱ�ΪE��F��CG��AB���ϵĸߣ�
��1����D����BC��ʲôλ��ʱ��DE=DF����˵�����ɣ�
��2��DE��DF��CG�ij�֮������������ĵ�����ϵ����˵������.
��3����D�ڵױ�BC���ӳ����ϣ���2���еĽ��ۻ������������������ִ��������Ĺ�ϵ����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ij��������߷ֱ���2x��3��x��2��x�������ı����Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com