
【题目】(10分) 如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.

【答案】360°.
【解析】试题分析:连接BE,根据三角形外角的性质可得∠1=∠C+∠D=∠CBE+∠DEB,再由四边形的内角和定理可得∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F=360°.
试题解析:解:如图,连接BE.
∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
又∵∠A+∠ABE+∠BEF+∠F=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】问题情景:
如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.

小明的思路是:
过点P作PE//AB,

∴∠PAB+∠APE=180°.
∵∠PAB=130°,∴∠APE=50°
∵AB//CD,PE//AB,∴PE//CD,
∴∠PCD+∠CPE=180°.
∵∠PCD=120°,∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
如果AB与CD平行关系不变,动点P在直线AB、CD所夹区域内部运动时,∠PAB,∠PCD的度数会跟着发生变化.
(1)如图3,当动点P运动到直线AC右侧时,请写出∠PAB,∠PCD和∠APC之间的数量关系?并说明理由.

(2)如图4,AQ,CQ分别平分∠PAB,∠PCD,那么∠AQC和角∠APC有怎择的数量关系?

(3)如图5,点P在直线AC的左侧时,AQ,CQ仍然平分∠PAB,∠PCD,请直接写出∠AQC和角∠APC的数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:


请根据所给信息,解答下列问题:
(1)a=__________,b=__________;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低.就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离 (因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个求距离MN的方案,要求: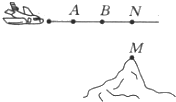
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
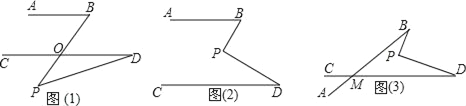
【题目】(1)如图(1),AB∥CD,点P在AB,CD外部,若∠B=50°,∠D=25°,则∠BPD= °
(2)如图(2),AB∥CD,点P在AB,CD内部,则∠B,∠D,∠BPD之间有何数量关系?证明你的结论.
(3)在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y1=k1x与反比例函数y2= ![]() 相交于A、B点.已知点A的坐标为A(4,n),BD⊥x轴于点D,且S△BDO=4.过点A的一次函数y3=k3x+b与反比例函数的图象交于另一点C,与x轴交于点E(5,0).
相交于A、B点.已知点A的坐标为A(4,n),BD⊥x轴于点D,且S△BDO=4.过点A的一次函数y3=k3x+b与反比例函数的图象交于另一点C,与x轴交于点E(5,0). 
(1)求正比例函数y1、反比例函数y2和一次函数y3的解析式;
(2)结合图象,求出当k3x+b> ![]() >k1x时x的取值范围.
>k1x时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )

A. ![]() a2 B.
a2 B. ![]() a2 C.
a2 C. ![]() a2 D.
a2 D. ![]() a
a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com