
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3).反比例函数y1= 图象经过点C,一次函数y2 =ax+b的图象经过点A、C
图象经过点C,一次函数y2 =ax+b的图象经过点A、C
(1)求反比例函数与一次函数的解析式;
(2)观察图象,在第四项限内写出使得y1<y2成立的自变量x的取值范围;
(3)若点P是反比例函数图象上的一点,且△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标,

解:(1)∵点A的坐标为(0.2),点B的坐标为(0,-3).∴AB=5.
∵四边形ABCD为正方形,∴点C的坐标为(5,- 3).
∵反比例函数y= 的图象经过点C,
的图象经过点C,
∴一3=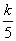 ,解得k= -15,∴反比例函数的解析式为y=-
,解得k= -15,∴反比例函数的解析式为y=-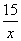 ;……(2分)
;……(2分)
∵一次函数的解析式为y=ax+b的图像经过点A,C,∴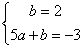 ,解得
,解得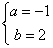
∴一次函数的解析式为y=-x+2;…………(4分)(2)0<x<5………………(6分)
(3)设P点的坐标为(x,y).∵△OAP的面积恰好等于正方形ABCD的面积,
∴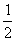 ×OA·|x|=52,∴
×OA·|x|=52,∴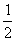 ×2|x| =25,解得x=±25.
×2|x| =25,解得x=±25.
当x=25时,y=-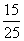 =-
=-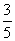 ;当x=-25时.Y=
;当x=-25时.Y=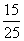 =
=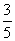
∴P点的坐标为(25,-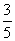 )或(-25,
)或(-25,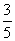 ).……(9分)
).……(9分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如右图矩形ABCD中.AD=8cm.AB= 6cm.动点E从点C开始 沿边CB向点B以2cm/s的速度运动至点B停止,动点F从点C 同时出发沿边CD向点D以1cm/s的速度运动至点D停止,如 图可得到矩形CFHE.设运动时间为x(单位:s).此时矩形ABCD 去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图
象表示大致是下图中的 ( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com