
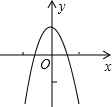 二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为( )
二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为( )| A. | y=-3x2-1 | B. | y=3x2 | C. | y=3x2+1 | D. | y=3x2-1 |
分析 由于二次函数y=-3x2+1的图象沿x轴翻折后所得抛物线的开口大小与原抛物线的开口大小相同,只是开口方向相反,然后写出点(0,1)关于x轴的对称点的坐标,再利用顶点式即可得到新抛物线的解析式.
解答 解:二次函数y=-3x2+1的图象的顶点坐标为(0,1),
点(0,1)关于x轴的对称点的坐标为(0,-1),
又因为二次函数y=-3x2+1的图象沿x轴翻折后所得抛物线的开口大小与原抛物线的开口大小相同,只是开口方向相反,
所以所得抛物线的解析式为y=3x2-1.
故选D.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左移动1个单位,向上移动3个单位 | |
| B. | 向右移动1个单位,向上移动3个单位 | |
| C. | 向左移动1个单位,向下移动3个单位 | |
| D. | 向右移动1个单位,向下移动3个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+1)2-1 | B. | y=2(x-1)2-1 | C. | y=2x2+1 | D. | y=2x2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com