
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 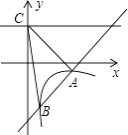
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
【答案】
(1)解:把A(2,﹣1)代入反比例解析式得:﹣1= ![]() ,即m=﹣2,
,即m=﹣2,
∴反比例解析式为y=﹣ ![]() ,
,
把B( ![]() ,n)代入反比例解析式得:n=﹣4,即B(
,n)代入反比例解析式得:n=﹣4,即B( ![]() ,﹣4),
,﹣4),
把A与B坐标代入y=kx+b中得: 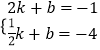 ,
,
解得:k=2,b=﹣5,
则一次函数解析式为y=2x﹣5;
(2)解:∵A(2,﹣1),B( ![]() ,﹣4),直线AB解析式为y=2x﹣5,
,﹣4),直线AB解析式为y=2x﹣5,
∵C(0,2),直线BC解析式为y=﹣12x+2,
将y=﹣1代入BC的解析式得x= ![]() ,则AD=2﹣
,则AD=2﹣ ![]() =
= ![]() .
.
∵xC﹣xB=2﹣(﹣4)=6,
∴S△ABC= ![]() ×AD×(yC﹣yB)=
×AD×(yC﹣yB)= ![]() ×
× ![]() ×6=
×6= ![]() .
.

【解析】(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,再将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;(2)利用两点间的距离公式求出AB的长,利用点到直线的距离公式求出点C到直线AB的距离,即可确定出三角形ABC面积.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】在质量检测中,从每盒标准质量为125克的酸奶中,抽取6盒,结果如下:
编号 | 1 | 2 | 3 | 4 | 5 | 6 |
质量(克) | 126 | 127 | 124 | 126 | 123 | 125 |
差值(克) | +1 |
(1)补全表格中相关数据;
(2)请你利用差值列式计算这6盒酸奶的质量和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t=________s时,△POQ是等腰三角形;当t=_______s时,△POQ是直角三角形.
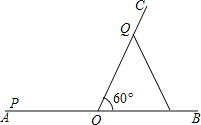
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
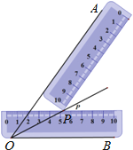
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 三角形三条垂直平分线的交点到三个定点的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表 | |||||
项目 | 篮球 | 足球 | 乒乓球 | 排球 | 羽毛球 |
人数 | a | 6 | 5 | 7 | 6 |
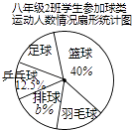
根据图中提供的信息,解答下列问题:
(1)a= , b=;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知∠1+∠2=180o, ∠3=∠B, 试说明∠DEC+∠C=180o. 请完成下列填空:
解:∵∠1+∠2=180o(已知)
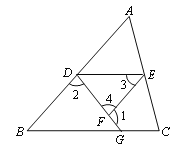
又∵∠1+ =180o(平角定义)
∴∠2= (同角的补角相等)
∴ (内错角相等,两直线平行)
∴∠3 = (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴ (等量代换)
∴ ∥ ( )
∴∠DEC+∠C=180o( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图放置,下列结论:①∠1=∠3;②若BC∥AD,则∠4=∠3;③若∠2=15°,必有∠4=2∠D;④若∠2=30°,则有AC∥DE. 其中正确的有_____.
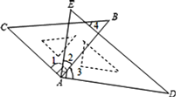
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF. 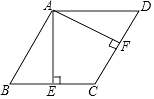
(1)求证:四边形ABCD是菱形;
(2)若∠EAF=60°,CF=2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com