
【题目】一副三角板按如图放置,下列结论:①∠1=∠3;②若BC∥AD,则∠4=∠3;③若∠2=15°,必有∠4=2∠D;④若∠2=30°,则有AC∥DE. 其中正确的有_____.
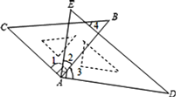
【答案】①③④
【解析】
根据余角的概念和同角的余角相等判断①;根据平行线的性质判断②;根据三角形的外角性质计算判断③;平行线的判定定理判断④.
解: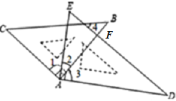
由题意可知∠CAB=∠EAD=90°,∠B=∠C=45°,∠D=30°,∠E=60°,
∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,故①正确;
若BC∥AD,
∠3与∠4既不是同位角,也不是内错角,无法证明∠4=∠3,故②错误;
若∠2=15°,
∴∠EFB=∠2+∠E=15°+60°=75°,
∴∠4=180°﹣∠EFB﹣∠B=180°﹣75°﹣45°=60°,
∵∠D=30°,
∴∠4=2∠D,故③正确;
若∠2=30°,则∠1=∠3=90°﹣30°=60°,
∴∠CAD=∠1+∠2+∠3=150°,
∵∠CAD+∠D=150°+30°=180°,
∴AC∥DE(同旁内角互补,两直线平行).故④正确.
故答案为:①③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 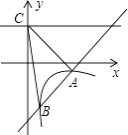
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )

A. 10 B. 6 C. 4 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对“隔离直线”给出如下定义:
点P(x,m)是图形G1上的任意一点,点Q(x,n)是图形G2上的任意一点,若存在直线l:kx+b(k≠0)满足m≤kx+b且n≥kx+b,则称直线l:y=kx+b(k≠0)是图形G1与G2的“隔离直线”.
如图1,直线l:y=﹣x﹣4是函数y= ![]() (x<0)的图象与正方形OABC的一条“隔离直线”.
(x<0)的图象与正方形OABC的一条“隔离直线”.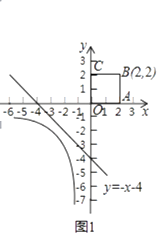
(1)在直线y1=﹣2x,y2=3x+1,y3=﹣x+3中,是图1函数y= ![]() (x<0)的图象与正方形OABC的“隔离直线”的为;
(x<0)的图象与正方形OABC的“隔离直线”的为;
请你再写出一条符合题意的不同的“隔离直线”的表达式:;
(2)如图2,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标是( ![]() ,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
(3)正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点M(1,t)是此正方形的中心.若存在直线y=2x+b是函数y=x2﹣2x﹣3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com