
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )

A. 10 B. 6 C. 4 D. 不确定
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”针对这种现象某媒体记者在多个路口采访闯红灯的行人,得出形成这种现象的四个基本原因,①红绿灯设置不科学,交通管理混乱占1%;②侥幸心态;③执法力度不够占9%;④从众心理,该记者将这次调查情况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题.
(1)该记者本次一共调査了名行人;
(2)求图1中④所在扇形的圆心角,并补全图2; 
(3)在本次调查中,记者随机采访其中的一名行人,求他属于第②种情况的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表 | |||||
项目 | 篮球 | 足球 | 乒乓球 | 排球 | 羽毛球 |
人数 | a | 6 | 5 | 7 | 6 |
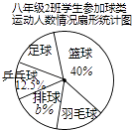
根据图中提供的信息,解答下列问题:
(1)a= , b=;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图放置,下列结论:①∠1=∠3;②若BC∥AD,则∠4=∠3;③若∠2=15°,必有∠4=2∠D;④若∠2=30°,则有AC∥DE. 其中正确的有_____.
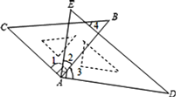
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2. 试说明DF∥AE. 请你完成下列填空,把解答过程补充完整.
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°( ).
∴∠CDA=∠DAB(等量代换).
又∠1=∠2,
从而∠CDA-∠1=∠DAB-________(等式的性质).
即∠3=_______.
∴DF∥AE( ).
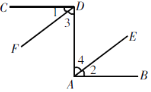
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF. 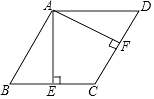
(1)求证:四边形ABCD是菱形;
(2)若∠EAF=60°,CF=2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.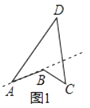
(1)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.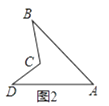
(2)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B=°.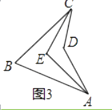
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,∠ACB=90°,CD为高,且CD、CE三等分∠ACB.
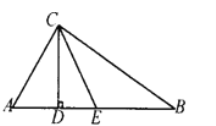
(1)求∠B的度数.
(2)求证:CE是AB边上的中线,且![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.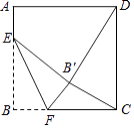
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com