
【题目】如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t=________s时,△POQ是等腰三角形;当t=_______s时,△POQ是直角三角形.
【答案】![]() 或10
或10 ![]()
【解析】
根据△POQ是等腰三角形,分两种情况进行讨论:点P在AO上,或点P在BO上;根据△POQ是直角三角形,分两种情况进行讨论:PQ⊥AB,或PQ⊥OC,据此进行计算即可.
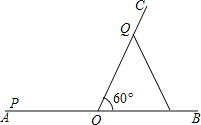
如图,当PO=QO时,△POQ是等腰三角形
∵PO=AOAP=102t,OQ=1t
∴当PO=QO时,102t=t
解得t=![]() ;
;
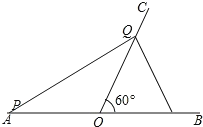
如图,当PO=QO时,△POQ是等腰三角形
∵PO=APAO=2t10,OQ=1t
∴当PO=QO时,2t10=t
解得t=10;
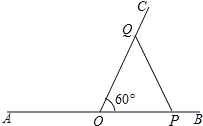
如图,当PQ⊥AB时,△POQ是直角三角形,且QO=2OP
∵PO=APAO=2t10,OQ=1t,
∴当QO=2OP时,t=2×(2t10)
解得t=![]() ;
;
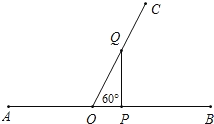
如图,当PQ⊥OC时,△POQ是直角三角形,且2QO=OP
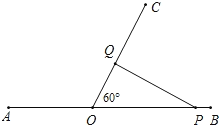
∵PO=APAO=2t10,OQ=1t,
∴当2QO=OP时,2t=2t10
方程无解.
故答案为:(1). ![]() 或10 (2).
或10 (2). ![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】分别写有数0,2﹣1 , ﹣2,cos30°,3的五张卡片,除数字不同外其他均相同,从中任意抽取一张,那么抽到非负数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 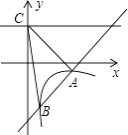
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对“隔离直线”给出如下定义:
点P(x,m)是图形G1上的任意一点,点Q(x,n)是图形G2上的任意一点,若存在直线l:kx+b(k≠0)满足m≤kx+b且n≥kx+b,则称直线l:y=kx+b(k≠0)是图形G1与G2的“隔离直线”.
如图1,直线l:y=﹣x﹣4是函数y= ![]() (x<0)的图象与正方形OABC的一条“隔离直线”.
(x<0)的图象与正方形OABC的一条“隔离直线”.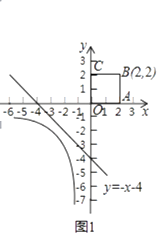
(1)在直线y1=﹣2x,y2=3x+1,y3=﹣x+3中,是图1函数y= ![]() (x<0)的图象与正方形OABC的“隔离直线”的为;
(x<0)的图象与正方形OABC的“隔离直线”的为;
请你再写出一条符合题意的不同的“隔离直线”的表达式:;
(2)如图2,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标是( ![]() ,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
(3)正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点M(1,t)是此正方形的中心.若存在直线y=2x+b是函数y=x2﹣2x﹣3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,请直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com