
����Ŀ�����壺��һ���ڱ���ȣ��������ǵļн���ֱ�ǵ��ı��ν�������ֱ���ı���.
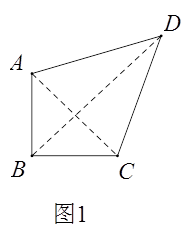
��1����ͼ1������ֱ���ı���ABCD��AB=BC����ABC=90�㣬
����AB=CD=1��AB//CD����Խ���BD�ij�.
����AC��BD����֤��AD=CD.
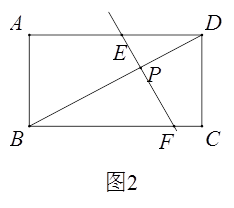
��2����ͼ2���ھ���ABCD�У�AB=5��BC=9����P�ǶԽ���BD��һ�㣬��BP=2PD������P��ֱ�߷ֱ�AD��BC�ڵ�E��F��ʹ�ı���ABFE�ǵ���ֱ���ı���.��AE�ij�.
���𰸡�
��1��
�⣺����ΪAB=CD=1��AB//CD,
�����ı���ABCD��ƽ���ı���.
����ΪAB=BC��
������ABCD������.
����Ϊ��ABC=90�ȣ�
��������ABCD��������.
����BD= ![]() .
.
����ͼ1������AC��BD��
��ΪAB=BC��AC��BD��
���ԡ�ABD=��CBD,
����ΪBD=BD��
���ԡ�ABD��CBD��
����AD=CD.
��2��
�⣺��EF��BC��ֱ����AE��EF��BF��EF��
�����ı���ABFE���ǵ���ֱ���ı��Σ�������������
��EF��BC����ֱ��
�ٵ�AE=ABʱ����ͼ2��
��ʱ�ı���ABFE�ǵ���ֱ���ı���.
����AE=AB=5.
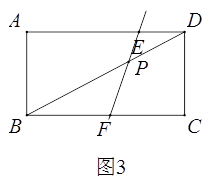
�ڵ�BF=ABʱ����ͼ3��
��ʱ�ı���ABFE�ǵ���ֱ���ı���.
����BF=AB=5��
��ΪDE//BF��
���ԡ�PED~��PFB��
����DE��BF=PD��PB=1:2,
����AE=9-2.5=6.5.
����������AE�ij�Ϊ5��6.5.
����������1������AB=CD=1��AB//CD,���ݡ���һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Ρ��ɵ��ı���ABCD��ƽ���ı���.���ڱ����AB=BC����һֱ�ǡ�ABC=90�ȣ���������ABCD��������.��BD= ![]() ��������AC��BD����AB=BC��AC��BD����֪�ı���ABCD��һ�����Σ���ֻҪ֤����ABD��CBD�����ɵõ�AD=CD.��2���������ۣ���EF��BC��ֱ����ʾ��AE��EF��BF��EF����EF�������ڱ߲���ȣ��ɡ�A=��ABC=90�㣬�ɷ�������AB=AEʱ��AB=BFʱȥ���.
��������AC��BD����AB=BC��AC��BD����֪�ı���ABCD��һ�����Σ���ֻҪ֤����ABD��CBD�����ɵõ�AD=CD.��2���������ۣ���EF��BC��ֱ����ʾ��AE��EF��BF��EF����EF�������ڱ߲���ȣ��ɡ�A=��ABC=90�㣬�ɷ�������AB=AEʱ��AB=BFʱȥ���.
�����㾫����������Ĺؼ���������ƽ���ı��ε��ж������֪ʶ����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı��Σ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ![]() ��x��0����ͼ����A��2����1����B��
��x��0����ͼ����A��2����1����B�� ![]() ��n�����㣬ֱ��y=2��y�ύ�ڵ�C��
��n�����㣬ֱ��y=2��y�ύ�ڵ�C�� 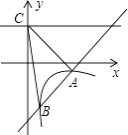
��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У��ԡ�����ֱ�ߡ��������¶��壺
��P��x��m����ͼ��G1�ϵ�����һ�㣬��Q��x��n����ͼ��G2�ϵ�����һ�㣬������ֱ��l��kx+b��k��0������m��kx+b��n��kx+b�����ֱ��l��y=kx+b��k��0����ͼ��G1��G2�ġ�����ֱ�ߡ���
��ͼ1��ֱ��l��y=��x��4�Ǻ���y= ![]() ��x��0����ͼ����������OABC��һ��������ֱ�ߡ���
��x��0����ͼ����������OABC��һ��������ֱ�ߡ���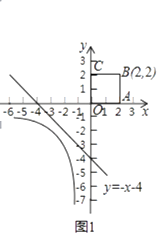
��1����ֱ��y1=��2x��y2=3x+1��y3=��x+3�У���ͼ1����y= ![]() ��x��0����ͼ����������OABC�ġ�����ֱ�ߡ���Ϊ��
��x��0����ͼ����������OABC�ġ�����ֱ�ߡ���Ϊ��
������д��һ����������IJ�ͬ�ġ�����ֱ�ߡ��ı���ʽ����
��2����ͼ2����һ���ĵ���ֱ��������EDF�������ֱ���������ƽ�У�ֱ�Ƕ���D�������ǣ� ![]() ��1������O�İ뾶Ϊ2���Ƿ���ڡ�EDF���O�ġ�����ֱ�ߡ��������ڣ�����ˡ�����ֱ�ߡ��ı���ʽ���������ڣ���˵�����ɣ�
��1������O�İ뾶Ϊ2���Ƿ���ڡ�EDF���O�ġ�����ֱ�ߡ��������ڣ�����ˡ�����ֱ�ߡ��ı���ʽ���������ڣ���˵�����ɣ�
��3��������A1B1C1D1��һ����y���ϣ��������߶���y����Ҳ࣬��M��1��t���Ǵ������ε����ģ�������ֱ��y=2x+b�Ǻ���y=x2��2x��3��0��x��4����ͼ����������A1B1C1D1�ġ�����ֱ�ߡ�����ֱ��д��t��ȡֵ��Χ��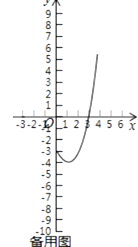
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ�1����ABA1�У���B��20�㣬AB��A1B����A1B��ȡһ��C���ӳ�AA1��A2��ʹ��A1A2��A1C����A2C��ȡһ��D���ӳ�A1A2��A3��ʹ��A2A3��A2D��������������������ȥ����n�������ε���AnΪ������ڽǵĶ���Ϊ______��
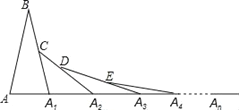
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AD����ô��������һ�������������ж���ABC�ա�ADC���ǣ�������

A. CB=CD B. ��BAC=��DAC C. ��BCA=��DCA D. ��B=��D=90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı��β�ƺABCD�У���B=90�㣬AB=24m��BC=7m��CD=15m��AD=20m.
��1���ж���ADC�Ƿ���ֱ�ǣ���˵��������
��2�������ı��β�ƺABCD�����.
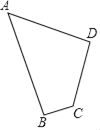
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У�������Ϊ�ж���ABD�ա�BAC�������ǣ� )

A. ��D����C����BAD����ABC B. ��BAD����ABC����ABD����BAC
C. BD��AC����BAD����ABC D. AD��BC��BD��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����Ƕ����P��a��b���ġ��任�㡱ΪQ���ҹ涨����a��bʱ��QΪ��b����a������a��bʱ��QΪ��a����b����
��1���㣨2��1���ı任������Ϊ��
��2������A��a����2���ı任���ں���y= ![]() ��ͼ���ϣ���a��ֵ��
��ͼ���ϣ���a��ֵ��
��3����ֱ֪��l�������ύ�ڣ�6��0������0��3�����㣮��ֱ��l�����е�ı任�����һ���µ�ͼ�μ���M�� �ж�������y=x2+c��ͼ��M�Ľ���������Լ���Ӧ��c��ȡֵ��Χ����ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
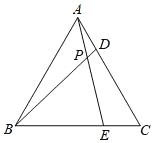
����Ŀ����ͼ����ABC Ϊ�ȱ������Σ�D��E �ֱ��DZ� AC��BC �ϵĵ㣬��AD��CE��AE �� BD �ཻ�ڵ� P.
��1�����BPE �Ķ�����
��2���� BF��AE �ڵ� F�����ж� BP �� PF ��������ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com