
【题目】在平面直角坐标系中,我们定义点P(a,b)的“变换点”为Q.且规定:当a≥b时,Q为(b,﹣a);当a<b时,Q为(a,﹣b).
(1)点(2,1)的变换点坐标为;
(2)若点A(a,﹣2)的变换点在函数y= ![]() 的图象上,求a的值;
的图象上,求a的值;
(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的变换点组成一个新的图形记作M. 判断抛物线y=x2+c与图形M的交点个数,以及相应的c的取值范围,请直接写出结论.
【答案】
(1)(1,﹣2)
(2)
解:当a≥﹣2时,则A(a,﹣2)的变换点坐标为(﹣2,﹣a),
代入y= ![]() 可得﹣a=
可得﹣a= ![]() ,解得a=
,解得a= ![]() ;
;
当a<﹣2时,则A(a,﹣2)的变换点坐标为(a,2),
代入y= ![]() 可得2=
可得2= ![]() ,解得a=
,解得a= ![]() ,不符合题意;
,不符合题意;
综上可知a的值为 ![]() ;
;
(3)
解:设直线l的解析式为y=kx+b (k≠0 ),将点(6,0)、(0,3)代入y=kx+b得: ![]() ,解得
,解得 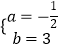 ,
,
∴直线l的解析式为y=﹣ ![]() x+3.
x+3.
当x=y时,x=﹣ ![]() x+3,解得x=2.
x+3,解得x=2.
点C的坐标为(2,﹣2),点C的变换点的坐标为C′( 2,﹣2 ),
点(6,0)的变换点的坐标为(0,﹣6),点(0,3)的变换点的坐标为(0,﹣3),
当x≥2时,所有变换点组成的图形是以C′( 2,﹣2)为端点,过(0,﹣6 )的一条射线;即:y=2x﹣6,其中x≥2,
当x<2时,所有变换点组成的图形是以C′(2,﹣2)为端点,过(0,﹣3)的一条射线,即y= ![]() x﹣3,其中,x<2.
x﹣3,其中,x<2.
所以新的图形M是以C′(2,﹣2)为端点的两条射线组成的图形.
如图所示:
由  和
和 ![]() 得:x2﹣
得:x2﹣ ![]() x+c+3=0①和x2﹣2x+c+6=0②
x+c+3=0①和x2﹣2x+c+6=0②
讨论一元二次方程根的判别式及抛物线与点C′的位置关系可得:
①当方程①无实数根时,即:当c>﹣ ![]() 时,抛物线y=x2+c与图形M没有交点;
时,抛物线y=x2+c与图形M没有交点;
②当方程①有两个相等实数根时,即:当c=﹣ ![]() 时,抛物线y=x2+c与图形M有一个交点;
时,抛物线y=x2+c与图形M有一个交点;
③当方程②无实数根,且方程①有两个不相等的实数根时,即:当﹣5<c<﹣ ![]() 时,抛物线y=x2+c与图形M有两个交点;
时,抛物线y=x2+c与图形M有两个交点;
④当方程②有两个相等实数根或y=x2+c恰好经过经过点C′时,即:当c=﹣5或c=﹣6时,抛物线y=x2+c与图形M有三个交点;
⑤当方程②方程①均有两个不相等的实数根时,且两根均小于2,即:当﹣6<c<﹣5时,抛物线y=x2+c与图形M有四个交点;
⑥当c<﹣6时,抛物线y=x2+c与图形M有两个交点.
【解析】解:(1)∵2≥﹣1,
∴点(2,1)的变换点坐标为(1,﹣2),
所以答案是:(1,﹣2);
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF. 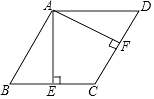
(1)求证:四边形ABCD是菱形;
(2)若∠EAF=60°,CF=2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( ) 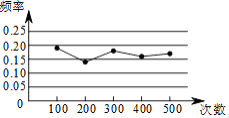
A.袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B.掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D.掷一枚质地均匀的硬币,落地时结果是“正面向上”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.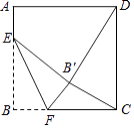
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OC、OA分别与x轴,y轴重合,连接OB,将长方形纸片OABC沿OB折叠,使点A落在点A,的位置,A,B与x轴交于D,若点B的坐标为(4,2),则点A,的坐标为( )
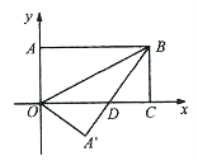
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年秋,珊瑚中学开启“珊中大阅读”活动,为了充实漂流书吧藏书,号召全校学生捐书,得到各班的大力支持.同时,本部校区的两个年级组也购买藏书充实学校图书室,初二年级组购买了甲、乙两种自然科学书籍若干本,用去8315元;初一年级买了A、B两种文学书籍若干本,用去6138元。其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲种书的单价比乙种书的单价多7元,则甲种书籍比乙种书籍多买了_____________本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1为北京城市女生从出生到15岁的平均身高统计图,图2是北京城市某女生从出生到12岁的身高统计图. 
请你根据以上信息预测该女生15岁时的身高约为 , 你的预测理由是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com