练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】图1为北京城市女生从出生到15岁的平均身高统计图，图2是北京城市某女生从出生到12岁的身高统计图．
    请你根据以上信息预测该女生15岁时的身高约为 ， 你的预测理由是 ．

    【答案】170厘米；12岁时该女生比平均身高高8厘米，预测她15岁时也比平均身高高8厘米
    【解析】解：根据以上信息预测该女生15岁时的身高约为170厘米， 预测的理由是：12岁时该女生比平均身高高8厘米，预测她15岁时也比平均身高高8厘米，
    所以答案是：170厘米，12岁时该女生比平均身高高8厘米，预测她15岁时也比平均身高高8厘米．
    【考点精析】根据题目的已知条件，利用折线统计图的相关知识可以得到问题的答案，需要掌握能清楚地反映事物的变化情况，但是不能清楚地表示出在总体中所占的百分比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，我们定义点P（a，b）的“变换点”为Q．且规定：当a≥b时，Q为（b，﹣a）；当a＜b时，Q为（a，﹣b）．
    （1）点（2，1）的变换点坐标为；
    （2）若点A（a，﹣2）的变换点在函数y= 的图象上，求a的值；
    （3）已知直线l与坐标轴交于（6，0），（0，3）两点．将直线l上所有点的变换点组成一个新的图形记作M． 判断抛物线y=x2+c与图形M的交点个数，以及相应的c的取值范围，请直接写出结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

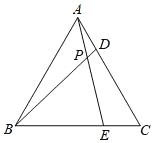
    【题目】如图，△ABC 为等边三角形，D、E 分别是边 AC、BC 上的点，且AD＝CE，AE 与 BD 相交于点 P.

    （1）求∠BPE 的度数；

    （2）若 BF⊥AE 于点 F，试判断 BP 与 PF 的数量关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务，分为A、B、C、D四种型号，它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示：
    根据以上信息，下列判断错误的是（ ）
    A.其中的D型帐篷占帐篷总数的10%
    B.单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍
    C.单独生产A型帐篷与单独生产D型帐篷的天数相等
    D.单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一张三角形纸片ABC，其中∠C=90°，AC=6，BC=8．小静同学将纸片做两次折叠：第一次使点A落在C处，折痕记为m；然后将纸片展平做第二次折叠，使点A落在B处，折痕记为n．则m，n的大小关系是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD和正方形DEFG中，顶点B、D、F在同一直线上，H是BF的中点．
    （1）如图1，若AB=1，DG=2，求BH的长；

    （2）如图2，连接AH，GH．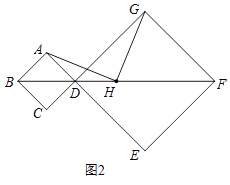

    小宇观察图2，提出猜想：AH=GH，AH⊥GH．小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
    想法1：延长AH交EF于点M，连接AG，GM，要证明结论成立只需证△GAM是等腰直角三角形；
    想法2：连接AC，GE分别交BF于点M，N，要证明结论成立只需证△AMH≌△HNG．
    …
    请你参考上面的想法，帮助小宇证明AH=GH，AH⊥GH．（一种方法即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠A=30°，∠B=62°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，求∠CDF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

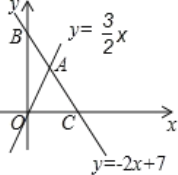
    【题目】如图，直线y=﹣2x+7与x轴、y轴分别相交于点C、B，与直线y=x相交于点A．

    (1)求A点坐标；

    (2)求△OAC的面积；

    (3)如果在y轴上存在一点P，使△OAP是以OA为底边的等腰三角形，求P点坐标；

    (4)在直线y=﹣2x+7上是否存在点Q，使△OAQ的面积等于6？若存在，请求出Q点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某风景区门票价格如图所示，某旅行社有甲、乙两个旅行团队，计划在“五一”小黄金周期间到该景点游玩，两团队游客人数之和为120人，乙团队人数不超过50人．设甲团队人数为x人，如果甲、乙两团队分别购买门票，两团队门票款之和为W元．
    （1）求W关于x的函数关系式，并写出自变量x 的取值范围；
    （2）若甲团队人数不超过100人，请说明甲、乙两团队联合购票比分别购票最多可节约多少元．

    查看答案和解析>>

    同步练习册答案