
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠PBC=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠PBC=∠C.分析 (1)根据同圆中,同弧所对的圆周角相等可得∠P=∠C,再由条件∠C=∠PBC可得∠P=∠PBC,然后可得CB∥PD;
(2)根据垂径定理可得CE=4,在Rt△COE中,根据勾股定理可得方程x2=42+(x-2)2,再解即可.
解答 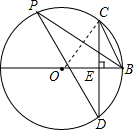 解:(1)∵∠P=∠C,∠C=∠PBC,
解:(1)∵∠P=∠C,∠C=∠PBC,
∴∠P=∠PBC,
∴CB∥DP;
(2)连接CO,设CO=x,则BO=x,
∵弦CD⊥AB于点E,CD=8,
∴CE=4,
∵BE=2,
∴EO=x-2,
在Rt△COE中:CO2=CE2+OE2,
∴x2=42+(x-2)2,
解得:x=5,
∴⊙O的半径为5.
点评 此题主要考查了圆周角定理和垂径定理,以及勾股定理的应用,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
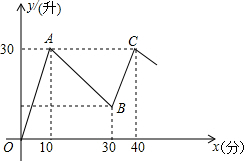 某工厂的一大型机器在进行加工作业时需供应冷却液进行降温,首先向冷却装置的储液箱中匀速输入冷却液,装满后开始向外输出冷却液为加工零件降温,同时加工作业开始,当储液箱中的冷却液下降到一定量后,开始向储液箱中补充输入冷却液,补充冷却液的过程中,加工作业同时进行,储液箱中的储液量y(升)与时间x(分)的函数关系如图所示
某工厂的一大型机器在进行加工作业时需供应冷却液进行降温,首先向冷却装置的储液箱中匀速输入冷却液,装满后开始向外输出冷却液为加工零件降温,同时加工作业开始,当储液箱中的冷却液下降到一定量后,开始向储液箱中补充输入冷却液,补充冷却液的过程中,加工作业同时进行,储液箱中的储液量y(升)与时间x(分)的函数关系如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com