
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,
有实数根,![]() 为正整数.
为正整数.
(1)求![]() 的值;
的值;
(2)当此方程有两个不为0的整数根时,将关于![]() 的二次函数
的二次函数![]() 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式;
(3)在(2)的条件下,将平移后的二次函数图象位于![]() 轴左侧的部分沿
轴左侧的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线![]() 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出![]() 的取值范围.
的取值范围.
【答案】(1) 1,2,3;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由![]() 求出正整数解即可.
求出正整数解即可.
(2)求出方程有两个不为0的整数根时的二次函数解析式,根据平移的性质得到平移后的函数图象的解析式.
(3)分直线![]() 与
与![]() 有一个交点且与
有一个交点且与![]() 有两个交点和直线
有两个交点和直线![]() 与
与![]() 有两个交点且与
有两个交点且与![]() 有一个交点两种情况求解即可.
有一个交点两种情况求解即可.
(1)∵ 方程有实数根,∴![]() .
.
∴![]() ,解得
,解得![]() .
.
∵![]() 为正整数,∴
为正整数,∴![]() 为1,2,3.
为1,2,3.
(2)当![]() 时,
时,![]() ,方程的两个整数根为6,0;
,方程的两个整数根为6,0;
当![]() 时,
时,![]() ,方程无整数根;
,方程无整数根;
当![]() 时,
时,![]() ,方程的两个整数根为2,1
,方程的两个整数根为2,1
∴![]() ,原抛物线的解析式为:
,原抛物线的解析式为:![]() .
.
∴平移后的图象的解析式为![]() .
.
(3)翻折后得到一个新的图象G的解析式为 ,
,
联立![]() 得
得![]() ,即
,即![]() .
.
由![]() 得
得![]() .
.
∴当![]() 或
或![]() 时,直线
时,直线![]() 与
与![]() 有一个交点,当
有一个交点,当![]() 时,直线
时,直线![]() 与
与![]() 有两个交点.
有两个交点.
联立![]() 得
得![]() ,即
,即![]() .
.
由![]() 得
得![]() .
.
∴当![]() 或
或![]() 时,直线
时,直线![]() 与
与![]() 有一个交点,当
有一个交点,当![]() 时,直线
时,直线![]() 与
与![]() 有两个交点.
有两个交点.
∴要使直线![]() 与图象G有3个公共点即要直线
与图象G有3个公共点即要直线![]() 与
与![]() 有一个交点且与
有一个交点且与![]() 有两个交点;或直线
有两个交点;或直线![]() 与
与![]() 有两个交点且与
有两个交点且与![]() 有一个交点.
有一个交点.
∴![]() 的取值范围为
的取值范围为![]() .
.


科目:初中数学 来源: 题型:
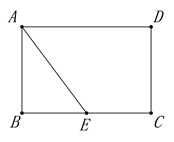
【题目】如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;
(3)探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件: .

备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E为BC上一点,F为CD上一点,且AE=AF.设△AEF的面积为y,CE=x.
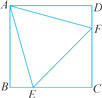
(第11题)
(1)求y关于x的函数表达式.
(2)当△AEF为正三角形时,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
(1)求∠C的度数;
(2)已知DF的长是关于![]() 的方程
的方程![]() -
-![]() -6=0的一个根,求该方程的另一个根.
-6=0的一个根,求该方程的另一个根.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
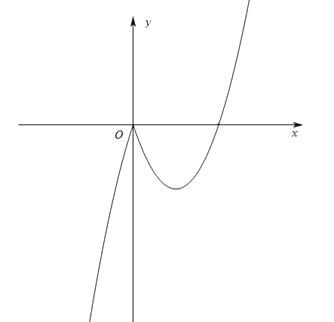
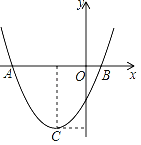
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(﹣1,﹣3),与x轴交于A(﹣3,0)、B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,每只利润为 元,该店每天可售出 只粽子.
(2)在不考虑其他因素的条件下,当零售单价下降多少元时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com