
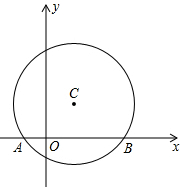
 如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧$\widehat{AB}$上.
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧$\widehat{AB}$上.分析 (1)根据垂径定理可得出AH=BH,然后在直角三角形ACH中可求出AH的长,再根据C点的坐标即可得出A、B两点的坐标.
(2)根据抛物线和圆的对称性,即可得出圆心C和P点必在抛物线的对称轴上,因此可得出P点的坐标为(1,3).然后可用顶点式二次函数通式来设抛物线的解析式.根据A或B的坐标即可确定抛物线的解析式.
(3)如果OP、CD互相平分,那么四边形OCPD是平行四边形.因此PC平行且相等于OD,那么D点在y轴上,且坐标为(0,2).然后将D点坐标代入抛物线的解析式中即可判定出是否存在这样的点.
解答 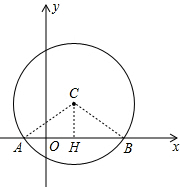 解:(1)如图,作CH⊥AB于点H,连接OA,OB,
解:(1)如图,作CH⊥AB于点H,连接OA,OB,
∵CH=1,半径CB=2
∴HB=$\sqrt{3}$,
故A(1-$\sqrt{3}$,0),B(1+$\sqrt{3}$,0).
(2)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3),
设抛物线解析式y=a(x-1)2+3,
把点B(1+$\sqrt{3}$,0)代入上式,解得a=-1;
∴y=-x2+2x+2.
(3)假设存在点D使线段OP与CD互相平分,则四边形OCPD是平行四边形
∴PC∥OD且PC=OD.
∵PC∥y轴,
∴点D在y轴上.
又∵PC=2,
∴OD=2,即D(0,2).
又D(0,2)满足y=-x2+2x+2,
∴点D在抛物线上
∴存在D(0,2)使线段OP与CD互相平分.
点评 本题是综合性较强的题型,所给的信息比较多,解决问题所需的知识点也较多,解题时必须抓住问题的关键点.二次函数和圆的综合,要求对圆和二次函数的性质在掌握的基础上灵活讨论运动变化,对解题技巧和解题能力的要求上升到一个更高的台阶.要求学生解题具有条理,挖出题中所隐含的条件,会分析问题,找出解决问题的突破口.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | -6 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
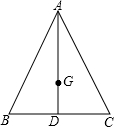 如图,已知△ABC中,AB=AC,tanB=2,AD⊥BC于点D,G是△ABC的重心,将△ABC绕着重心G旋转,得到△A1B1C1,并且点B1在直线AD上,联结CC1,那么tanCC1B1的值等于$\frac{\sqrt{13}-2}{3}$或$\frac{\sqrt{13}+2}{3}$.
如图,已知△ABC中,AB=AC,tanB=2,AD⊥BC于点D,G是△ABC的重心,将△ABC绕着重心G旋转,得到△A1B1C1,并且点B1在直线AD上,联结CC1,那么tanCC1B1的值等于$\frac{\sqrt{13}-2}{3}$或$\frac{\sqrt{13}+2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
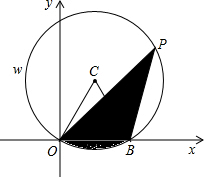 如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
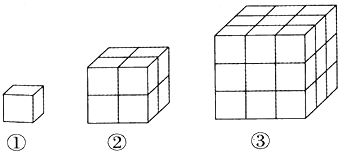
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
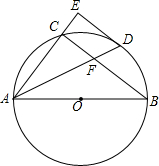 如图,AB是⊙O的直径,ED是⊙O的切线,D为切点,AE⊥DE,交⊙O于点C,垂足为E,连接AD.
如图,AB是⊙O的直径,ED是⊙O的切线,D为切点,AE⊥DE,交⊙O于点C,垂足为E,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
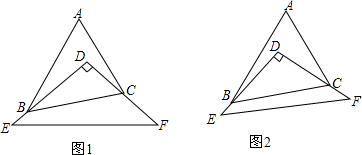
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com