
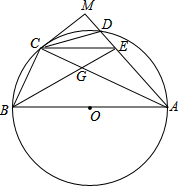
 如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.
如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.| AB2-BC2 |
| 142-62 |
| 10 |
| CG |
| AG |
| CE |
| AB |
| 7 |
| 14 |
| 1 |
| 2 |
| 2 |
| 3 |
8
| ||
| 3 |
| AC |
| AB |
4
| ||
| 14 |
2
| ||
| 7 |
2
| ||
| 7 |
| AG2+AE2-GE2 |
| 2AG•AE |
| AG2+AE2-GE2 |
| 2AG•AE |
2
| ||
| 7 |
8
| ||
| 3 |
| ||||
2×
|
2
| ||
| 7 |
| 121 |
| 9 |
| 11 |
| 3 |
| 11 |
| 3 |


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
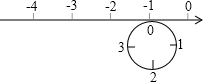 如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2014的点与圆周上表示数字几的点重合( )
如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2014的点与圆周上表示数字几的点重合( )| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
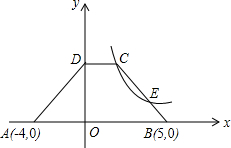 如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=
如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=| 3 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
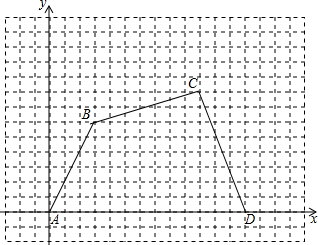 如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.你是怎样做的?
如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.你是怎样做的?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图①,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向移动.
如图①,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向移动.| m+2n-5 |
| 2m-n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com