
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下几种说法:
①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3. 9小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发![]() 小时再次与货车相遇;
小时再次与货车相遇;
其中正确的个数是_________. (填写序号)

【答案】①②③
【解析】
①根据函数的图象即可直接求解;②求得直线OA和DC的解析式,求得交点坐标即可.③设轿车从乙地出发x小时再次与货车相遇,根据题意列出方程解方程即可轿车与货车再次相遇的时间.
由图象可知:货车是匀速行驶,速度=300÷5=60千米/小时,故①正确;
设线段DC的解析式是y=kx+b,
根据题意得:
![]() 解得:
解得:![]() ,
,
则线段DC的解析式是:y=110x-195(2.5≤x≤4.5),
设OA的解析式是:y=mx,
根据题意得:5m=300,
解得:m=60,
则函数解析式是:y=60x,
根据题意得:
![]() 解得:
解得:![]() ,
,
则轿车与货车相遇时,货车恰好从甲地出发了3.9小时,故②正确;
设轿车从乙地出发x小时再次与货车相遇,
∵V货车=60千米/时,CD段V轿车=![]() (千米/时),
(千米/时),
∴110x+60(x+4.5)=300,
解得x=![]() (小时),故③正确.
(小时),故③正确.
故答案是:①②③.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),设其图象与x轴交于点A,B(A在B的左侧),点C在图象上,且S△ABC=1,求:
(1)求m;
(2)求点A,点B的坐标;
(3)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=y1﹣y2 , y1与x2成正比例,y2与x﹣1成反比例,当x=﹣1时,y=3;当x=2时,y=﹣3.
(1)求y与x之间的函数关系;
(2)当x= ![]() 时,求y的值.
时,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 已知a,b,c是三角形的三边,则a2+b2=c2
B. 在直角三角形中,两边的平方和等于第三边的平方
C. 在Rt△ABC中,∠![]() ,所以a2+b2=c2
,所以a2+b2=c2
D. 在Rt△ABC中,∠![]() ,所以a2+b2=c2
,所以a2+b2=c2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示. 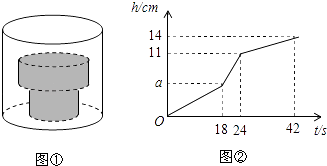
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为cm,匀速注水的水流速度为cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱的高和底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系. 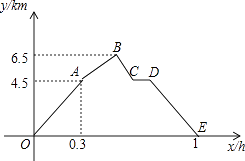
(1)小明骑车在平路上的速度为km/h;他途中休息了h;
(2)求线段AB、BC所表示的y与x之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的三角形中,不是直角三角形的是( )
A. ∠A+∠B=∠C B. ∠B=∠C=![]() ∠A
∠A
C. ∠A=90°-∠B D. ∠A-∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.

(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=ax2+bx+c如图所示,下列四个结论: ①abc<0;②b﹣2a<0;③a﹣b+c<0;④b2﹣4ac>0.
其中正确结论的个数是( )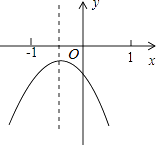
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com