
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.

(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
【答案】(1) ∠ABC=60°;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)根据等边三角形的判定得出△ABC是等边三角形,即可得出∠ABC的度数;
(2)根据BE=FE得出∠F=∠CEF=30°,再等边三角形的性质得出∠EBC=30°,即可证明;
(3)过E点作EG⊥BC,根据三角形面积解答即可.
试题解析:(1)∵BE⊥AC于E,E是AC的中点,
∴△ABC是等腰三角形,即AB=BC,
∵AB=AC,
∴△ABC是等边三角形,
∴∠ABC=60°;
(2)∵CF=CE,
∴∠F=∠CEF,
∵∠ACB=60°=∠F+∠CEF,
∴∠F=30°,
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=30°,
∴∠F=∠EBC,
∴BE=EF;
(3)过E点作EG⊥BC,如图:
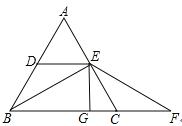
∵BE⊥AC,∠EBC=30°,AB=BC=2,
∴BE=![]() ,CE=1=CF,
,CE=1=CF,
在△BEC中,EG=![]() ,
,
∴![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
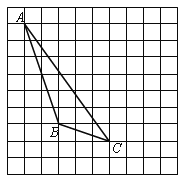
(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是: ;
(3)画出AB边上的高线CD;
(4)画出△ABC中AB边上的中线CE;
(5)△BCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究:
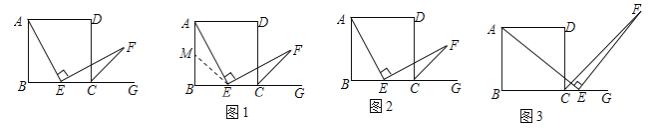
(1)、经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)、小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)、小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com