
 抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3).
抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3).分析 (1)根据已知点的坐标代入已知的函数的解析式即可利用待定系数法确定二次函数的解析式;
(2)首先根据平移确定平移后的函数的解析式,然后确定抛物线C2的顶点坐标;结合图形确定n的取值范围即可.
解答 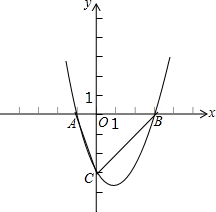 解:(1)∵抛物线C1:y=a(x+1)(x-3a)y轴交于点C(0,-3),
解:(1)∵抛物线C1:y=a(x+1)(x-3a)y轴交于点C(0,-3),
∴-3=a(0+1)(0-3a),
解得a=1(舍去负值).
∴抛物线C1的解析式为:y=(x+1)(x-3).
∴A(-1,0),B(3,0);
(2)∵y=(x+1)(x-3)=(x-1)2-4,
∴该抛物线的解析式为y=(x-1)2-4,则该抛物线的顶点坐标为(1,-4).
将(1)中求得的抛物线向上平移3个单位长度,
再向左平移n(n>0)个单位长度得到新抛物线y=(x-1+n)2-1,
∴平移后抛物线的顶点坐标是(1-n,-1),
∴-$\frac{2}{3}$<1-n<2,
解得-1<n<$\frac{5}{3}$,
∵n>0,
∴0<n<$\frac{5}{3}$.
点评 本题考查了二次函数图象与几何变换,题目中还渗透了数形结合的数学思想,这也是中考中常常出现的重要的数学思想,应加强此类题目的训练.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
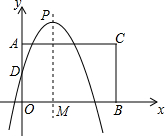 如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=-$\frac{3}{4}$x2+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M.
如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=-$\frac{3}{4}$x2+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
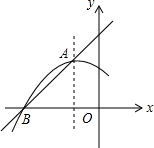 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )| A. | ①③④ | B. | ①③④⑤ | C. | ①③⑤ | D. | ②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
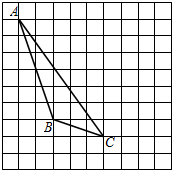 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图.查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:解答题
(14分) 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:判断题
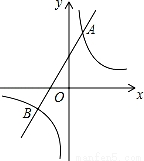
如图,已知反比例函数y= 的图象与一次函数
的图象与一次函数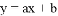 的图象相交于点A(1,4)和点B(n,-2).
的图象相交于点A(1,4)和点B(n,-2).
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:单选题
如图△ABC中,点D、E分别在边AB、AC上,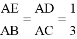 ,则
,则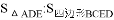 的值为( )
的值为( )
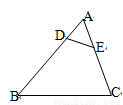
A. 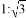 B. 1:3 C. 1:8 D. 1:9
B. 1:3 C. 1:8 D. 1:9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com